Декартовы координаты Задачи с решениями
Задачи с решениями

Вычислить расстояние от данной точки A(x0; y0) плоскости OXY до прямой ax + by + c = 0, если:
а) (x0; y0) = (1; 2); a = 4, b = 2, c = 2;
б) (x0; y0) = (1; 2); a = 4, b = 0, c = 2;
в) (x0; y0) = (1; 2); a = 0, b = 2, c = 2.
Решение
Проведем через точку A(x0; y0) прямую, перпендикулярную к данной прямой ax + by + c = 0. Уравнение этой прямой можно записать в виде (см. предыдущую задачу) –bx + ay + c1= 0. Так как точка A(x0; y0) принадлежит этой прямой, то –bx0 + ay0 + c1 = 0, и c1 = +(bx0 – ay0), и окончательно –b(x – x0) + a(y – y0) = 0. Решение системы
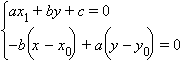 дает точку A(x; y) пересечения прямых (см. задачу 11.1):
дает точку A(x; y) пересечения прямых (см. задачу 11.1):
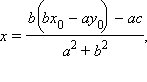
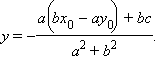 Тогда по теореме 11.2 расстояние от данной точки до данной прямой находится по формуле
Тогда по теореме 11.2 расстояние от данной точки до данной прямой находится по формуле
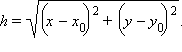 В нашем случае мы имеем
В нашем случае мы имеем
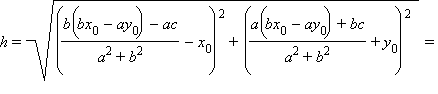
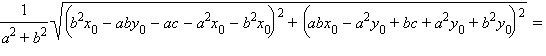
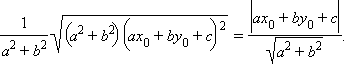 Это формула для вычисления расстояния от точки (x0; y0) до прямой ax + by + c = 0. Рассмотрим решение исходной задачи.
Это формула для вычисления расстояния от точки (x0; y0) до прямой ax + by + c = 0. Рассмотрим решение исходной задачи.
а)
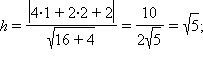
б)
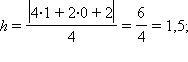
в)
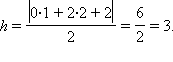
 5 из 24
5 из 24
 |


 Задачи с решениями
Задачи с решениями

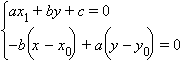 дает точку
дает точку 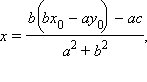
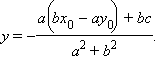 Тогда по теореме 11.2 расстояние от данной точки до данной прямой находится по формуле
Тогда по теореме 11.2 расстояние от данной точки до данной прямой находится по формуле
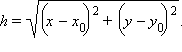 В нашем случае мы имеем
В нашем случае мы имеем
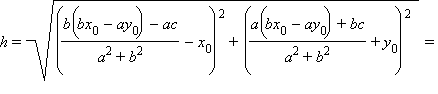
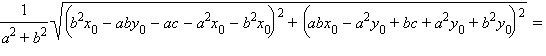
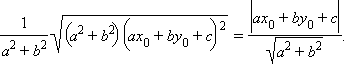 Это формула для вычисления расстояния от точки
Это формула для вычисления расстояния от точки 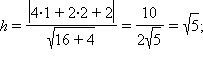
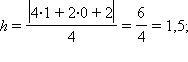
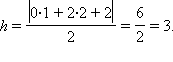
 5 из 24
5 из 24
