Декартовы координаты Задачи с решениями
Задачи с решениями

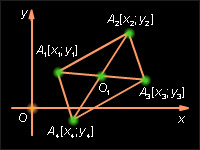
Показать, что если A1(x1; y1), A2(x2; y2), A3(x3; y3), A4(x4; y4) – последовательно вершины параллелограмма в плоскости OXY, то x2 – x1 = x3 – x4, y2 – y1 = y3 – y4.
Решение
По теореме 8.5 в точке пересечения O1 диагонали параллелограмма делятся пополам (см. рисунок). Следовательно, координаты точки O1 можно найти как координаты середин отрезков A1A3 и A2A4. На основании этого и теоремы 11.3 имеем
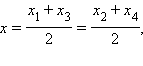
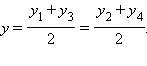 Отсюда имеем
Отсюда имеем
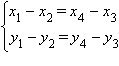 или
или
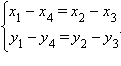
 6 из 24
6 из 24
 |


 Задачи с решениями
Задачи с решениями

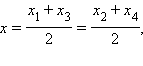
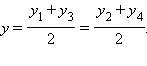 Отсюда имеем
Отсюда имеем
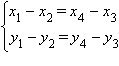 или
или
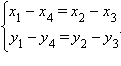
 6 из 24
6 из 24
