Декартовы координаты Задачи с решениями
Задачи с решениями

В окружность радиуса R вписан равносторонний треугольник. Доказать, что сумма квадратов расстояний от любой точки окружности до вершин треугольника постоянна, и найти эту сумму.
Решение
Шаг 1
Установим координаты вершин треугольника ABC: B(0; R),
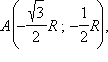
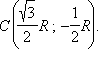 Окружность имеет уравнение: x2 + y2 = R2.
Окружность имеет уравнение: x2 + y2 = R2.
Шаг 2
Пусть T – произвольная точка на окружности.
Шаг 3
Согласно формуле расстояния между двумя точками
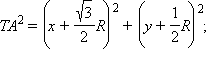 TB2 = x2 + (y – R)2;
TB2 = x2 + (y – R)2;
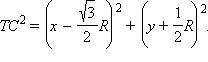 Поэтому
Поэтому
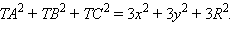 Учитывая, что точка T лежит на окружности, имеем: x2 + y2 = R2. Значит, TA2 + TB2 + TC2 = 3R2 + 3R2 = 6R2.
Учитывая, что точка T лежит на окружности, имеем: x2 + y2 = R2. Значит, TA2 + TB2 + TC2 = 3R2 + 3R2 = 6R2.
Ответ:
6R2.
 7 из 24
7 из 24
 |


 Задачи с решениями
Задачи с решениями

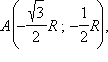
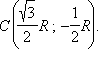 Окружность имеет уравнение:
Окружность имеет уравнение:  7 из 24
7 из 24
