

 Задачи с решениями
Задачи с решениями

Составить уравнение прямой, проходящей через две заданные точки
Первый способ. Так как точки 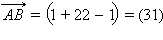 коллинеарен ей и, следовательно, ее можно считать направляющим вектором прямой. Тогда каноническое уравнение прямой (раздел 11.5) можно записать в виде
коллинеарен ей и, следовательно, ее можно считать направляющим вектором прямой. Тогда каноническое уравнение прямой (раздел 11.5) можно записать в виде 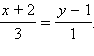 Отсюда получим
Отсюда получим
Второй способ. Общее уравнение прямой имеет вид
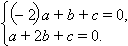
Решим эту систему относительно 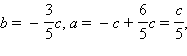 подставив найденные значения коэффициентов в исходное уравнение прямой имеем:
подставив найденные значения коэффициентов в исходное уравнение прямой имеем:
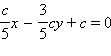 или окончательно
или окончательно 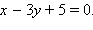
 16 из 25
16 из 25
 |