

 Задачи с решениями
Задачи с решениями

Составить уравнение прямой, проходящей через точку
а) 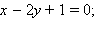 б)
б) 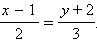
а) Прямая, перпендикулярная исходной прямой
б) Исходная прямая задана каноническим уравнением 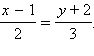 Направляющий векторэтой прямой равен (2; 3). Следовательно, направляющим вектором искомой прямой можно считать любой вектор диагональный вектору (2; 3), например, (3; –2). Так как искомая прямая проходит через точку (–3; 4), то ее каноническое уравнение можно задать так
Направляющий векторэтой прямой равен (2; 3). Следовательно, направляющим вектором искомой прямой можно считать любой вектор диагональный вектору (2; 3), например, (3; –2). Так как искомая прямая проходит через точку (–3; 4), то ее каноническое уравнение можно задать так 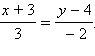
 17 из 25
17 из 25
 |