

 Задачи с решениями
Задачи с решениями

Установить, пересекаются, параллельны или совпадают данные пары прямых; в случае пересечения прямых найти координаты точки их пересечения:
а)
б)
в)
а) Найдем угловые коэффициенты прямых. Первое уравнение имеет вид 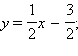 второе уравнение
второе уравнение 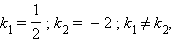 но
но 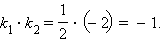 Следовательно (см теорему 11.13) прямые перпендикулярны и пересекаются. Для нахождения точки пересечения (общей точки) прямых решим совместно два уравнения
Следовательно (см теорему 11.13) прямые перпендикулярны и пересекаются. Для нахождения точки пересечения (общей точки) прямых решим совместно два уравнения

Отсюда получим 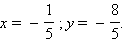
б) Умножим первое уравнение на (-2) и получим
в) Умножим первое уравнение на (-3) и получим
 19 из 25
19 из 25
 |