Задачи с решениями

Доказать, что, если стороны одного угла соответственно параллельны сторонам другого угла, то величины таких углов или равны, или в сумме составляют 180°.

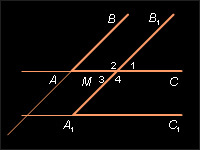
Пусть BAC и B₁A₁C₁ – данные углы и AB || A₁B₁, AC || A₁C₁ (см. рисунок).

Прямая A₁B₁ пересекает прямую A₁C₁, поэтому она пересекает параллельную ей прямую AC в некоторой точке M. При пересечении двух прямых образуются четыре угла, которые на рисунке обозначены 1, 2, 3, 4. Параллельные прямые AB и A₁B₁ пересечены секущей AM, поэтому данный угол BAC и один из углов 1, 2, 3, 4 являются накрест лежащими углами, и BAC равен одному из этих углов.

Аналогично параллельные прямые AC и A₁C₁ пересечены секущей A₁M, поэтому данный угол B₁A₁C₁ равен одному из углов 1, 2, 3, 4. У любых двух из этих четырех углов градусные меры либо равны, либо в сумме составляют 180°. Следовательно, или BAC = B₁A₁C₁, или BAC + B₁A₁C₁ = 180°.

1 из 6