Треугольник Задачи с решениями
Задачи с решениями

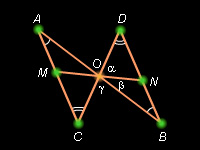
Отрезки AB и CD лежат на разных прямых и имеют общую середину O. Пусть M и N – середины отрезков AС и BD. Докажите, что O – середина отрезка MN.
Решение
Соединим точку O с точками M и N (см. рисунок).
Пусть  DON = α,
DON = α,  NOB = β,
NOB = β,  COB = γ. Oчевидно, α + β + γ = 180°, так как
COB = γ. Oчевидно, α + β + γ = 180°, так как  COD – развернутый. Треугольник AOС равен треугольнику BOD по двум сторонам и углу между ними. Действительно, по условию AO = OB, OD = OC, а
COD – развернутый. Треугольник AOС равен треугольнику BOD по двум сторонам и углу между ними. Действительно, по условию AO = OB, OD = OC, а  DOB =
DOB =  AOC как вертикальные. Следовательно,
AOC как вертикальные. Следовательно,  CAO =
CAO =  DBO,
DBO,  OCA =
OCA =  ODB, AC = BD. Отсюда
ODB, AC = BD. Отсюда 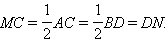 Рассмотрим треугольники OMС и OND. У них стороны OD = OC по условию, MC = ND и
Рассмотрим треугольники OMС и OND. У них стороны OD = OC по условию, MC = ND и  ODN =
ODN =  ODB =
ODB =  OCA =
OCA =  OCM. Поэтому ΔOMC = ΔOND по двум сторонам и углу между ними. Тогда
OCM. Поэтому ΔOMC = ΔOND по двум сторонам и углу между ними. Тогда  DON =
DON =  COM = α. Следовательно, величина угла MON равна
COM = α. Следовательно, величина угла MON равна  MOC + γ + β = α + β + γ = 180°, и угол MON – развернутый. Это значит, что точки M, O и N лежат на одной прямой. Кроме того, из равенства треугольников OMC и OND следует OM = ON. Следовательно, O – середина отрезка MN. Задача решена.
MOC + γ + β = α + β + γ = 180°, и угол MON – развернутый. Это значит, что точки M, O и N лежат на одной прямой. Кроме того, из равенства треугольников OMC и OND следует OM = ON. Следовательно, O – середина отрезка MN. Задача решена.
 1 из 6
1 из 6
 |


 Задачи с решениями
Задачи с решениями

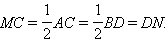 Рассмотрим треугольники
Рассмотрим треугольники  1 из 6
1 из 6
