Решение треугольников
Задачи с решениями
Внутри угла с вершиной O и величиной 60° дана точка A, отстоящая от сторон угла на расстояния a и b. Найти расстояние от точки A до вершины угла O.
Решение
Шаг 1
AB и AC – перпендикуляры, проведенные из точки A на стороны угла. По условию AB = a, AC = b.
Шаг 2
Продолжим отрезок BA до пересечения со стороной OC угла в точке D.
Шаг 3
Из треугольника OBD находим, что 
BDO = 30°. Из треугольника ACD находим, что AD = 2b (катет, лежащий против угла в 30°, равен половине гипотенузы).
Шаг 4
Отрезок BD равен a + 2b. Из треугольника DBO находим: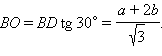 
Шаг 5
Из треугольника ABO по теореме Пифагора получаем
Ответ:
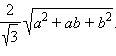
6 из 8
 |
