Окружность Задачи с решениями
Задачи с решениями

Из одной точки окружности проведены две хорды длиной 9 см и 17 см. Найти радиус окружности, если расстояние между серединами данных хорд равно 5 см.
Решение
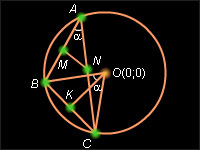
Пусть w (O, R) – данная окружность, AB и AC – искомые хорды, и, кроме того, величина угла BAC равна α (см. рисунок).
B треугольнике ABC M – середина стороны AB, N – середина стороны AC, следовательно, MN – средняя линия треугольника ABC, и по теореме 5.12 BC = 2MN = 10 см. По условию AB = 9 см, AC = 17 см, и по тереме косинусов имеем:
Угол BAC – вписанный в окружность w (O, R) и опирается на дугу BC, угол BOC – соответствующий ему центральный угол. По теореме 7.1 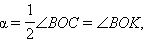 где OK – биссектриса угла BOC. Треугольник BOC равнобедренный (BO = OC = R), поэтому OK – его высота и медиана, а треугольник BOK прямоугольный. Поэтому
где OK – биссектриса угла BOC. Треугольник BOC равнобедренный (BO = OC = R), поэтому OK – его высота и медиана, а треугольник BOK прямоугольный. Поэтому 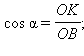
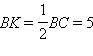 см. По теореме Пифагора
см. По теореме Пифагора
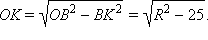 Cледовательно,
Cледовательно, 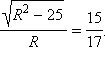 Oтсюда
Oтсюда
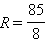 см. Задача решена.
см. Задача решена.
 3 из 6
3 из 6
 |


 Задачи с решениями
Задачи с решениями

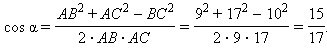
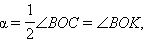 где
где 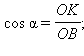
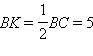
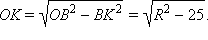 Cледовательно,
Cледовательно, 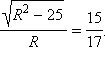 Oтсюда
Oтсюда
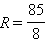 см. Задача решена.
см. Задача решена.
 3 из 6
3 из 6
