Окружность
Задачи с решениями
Дана окружность и точка M вне ее. Провести через точку M прямую, которая пересекает данную окружность в точках, расстояние между которыми дано.
Решение
Шаг 1
Пусть a – отрезок с данной длиной.
Шаг 2Анализ. Пусть прямая l пересекает данный круг по хорде AB данной длины (AB = a).
Шаг 3
Проведем перпендикуляр OC из центра O окружности на прямую l.
Шаг 4
Поскольку треугольник AOB равнобедренный, его высота OC является и медианой. Значит,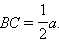 
Из треугольника OBC имеем:
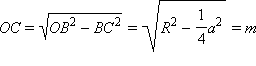– данная величина. Поскольку OM – данный отрезок, треугольник MCO можно построить по гипотенузе OM и катету OC.
Шаг 5Построение. Строим прямоугольный треугольник MCO по гипотенузе OM и катету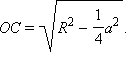 
Прямая MC – искомая.
Шаг 6Доказательство. Прямая MC пересекает данную окружность в точках A и B. OC – высота равнобедренного треугольника AOB. Из прямоугольного треугольника OBC имеем:
Задача решена.
4 из 6
 |
