Окружность
Задачи с решениями
Докажите теорему Птолемея: Если четырехугольник ABCD вписанный, то AC · BD = AB · CD + AD · BC. (Произведение диагоналей равно сумме произведений противоположных сторон.)
Решение
Шаг 1
На чертеже изображен данный четырехугольник ABCD, его диагонали и описанная около него окружность.
Шаг 2
Проведем из точки B отрезок BE до пересечения с диагональю AC таким образом, чтобы 
CBE = ABD.
Шаг 3
Углы BCA и BDA равны как вписанные, опирающиеся на дугу AB.
Шаг 4
Заметим, что треугольники ABD и EBC подобны, так как имеют равные углы. Отсюда следует, что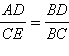 
и AD · BC = BD · CE (1).
Шаг 6
Сложим почленно равенства (1) и (2): AD · BC + AB · CD = BD · CE + BD · AE, AD · BC + AB · CD = BD · (CE + AE) = BD · AC, что и требовалось доказать.
5 из 6
 |
и 
