Задачи с решениями

Шаг 1

Пусть ABC – данный треугольник.

Шаг 2

Построим BO – медиану стороны AC. Продолжим ее на расстояние OD = BO. Достроим ΔABC до четырехугольника ABCD. Диагонали этого четырехугольника, пересекаясь, делятся пополам. Значит, этот четырехугольник – параллелограмм.

Шаг 3

Очевидно, CD = BA = 16 и AD = BC = 18. Таким образом, в параллелограмме ABCD известны стороны и диагональ AC. Требуется найти вторую диагональ BD.

Шаг 4

Известно, что в параллелограмме сумма квадратов сторон равна сумме квадратов диагоналей: 2·16² + 2·18² = 26² + BD²; 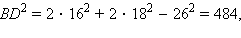откуда 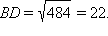  Далее заметим, что

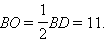
Ответ: BO = 11.