Четырехугольник Задачи с решениями
Задачи с решениями

Доказать, что высота равнобокой трапеции, в которую можно вписать окружность, является средним геометрическим ее оснований.
Решение
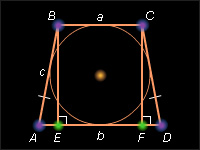
Так как в четырехугольнике, описанном около окружности, суммы длин противоположных сторон равны, то a + b = 2c, где a и b – длины оснований трапеции, а c – длина боковой стороны (см. рисунок).
Отсюда длина боковой стороны
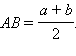 Далее имеем, что проекция боковой стороны на основание AD равна
Далее имеем, что проекция боковой стороны на основание AD равна
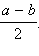 Действительно, прямоугольные треугольники ABE и CDF равны по катету (BE = CF) и гипотенузе (AB = CD). Поэтому AE = FD. Кроме того, EBCF – прямоугольник (BC || DA, EB || FC,
Действительно, прямоугольные треугольники ABE и CDF равны по катету (BE = CF) и гипотенузе (AB = CD). Поэтому AE = FD. Кроме того, EBCF – прямоугольник (BC || DA, EB || FC,  BEF = 90°), и, следовательно, EF = a. Отсюда имеем данное выражение для АЕ. Далее из прямоугольного треугольника ABE находим по теореме Пифагора BE2 = AB2 – AE2, то есть
BEF = 90°), и, следовательно, EF = a. Отсюда имеем данное выражение для АЕ. Далее из прямоугольного треугольника ABE находим по теореме Пифагора BE2 = AB2 – AE2, то есть
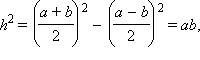 или
или
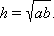
 3 из 6
3 из 6
 |


 Задачи с решениями
Задачи с решениями

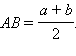 Далее имеем, что проекция боковой стороны на основание
Далее имеем, что проекция боковой стороны на основание 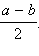 Действительно, прямоугольные треугольники
Действительно, прямоугольные треугольники 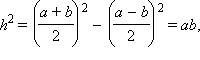 или
или
 3 из 6
3 из 6
