Четырехугольник Задачи с решениями
Задачи с решениями

Из вершины острого угла ромба проведены высоты к сторонам ромба, равные 3 см каждая, а расстояние между их основаниями равно 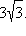 Вычислить длины диагоналей ромба.
Вычислить длины диагоналей ромба.
Решение
Пусть ABCD – данный ромб с острым углом α при вершине A, AM и AN – высоты ромба длины h, O – точка пересечения его диагоналей (см. рисунок).
В равнобедренном треугольнике MAN известны все стороны. По тереме косинусов вычислим величину косинуса угла MAN: 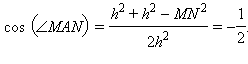 Отсюда
Отсюда  MAN = 120°. Диагональ AC ромба является его биссектрисой (теорема 8.6), поэтому
MAN = 120°. Диагональ AC ромба является его биссектрисой (теорема 8.6), поэтому  MCA =
MCA =  NCA = α/2. Треугольники AMC и ANC равны по катету и гипотенузе (AM = AN = h, AC – общая гипотенуза). Поэтому
NCA = α/2. Треугольники AMC и ANC равны по катету и гипотенузе (AM = AN = h, AC – общая гипотенуза). Поэтому  MAC =
MAC =  NAC. Но
NAC. Но  MAC +
MAC +  NAC =
NAC =  MAN = 120°. Отсюда
MAN = 120°. Отсюда  MAC = 60°.
MAC = 60°.
В прямоугольном треугольнике AMC:
1)  MAC +
MAC +  MCA = 90°. Отсюда
MCA = 90°. Отсюда 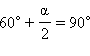 и α = 60°.
и α = 60°.
2)
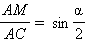 и
и
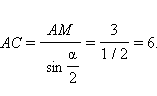 В прямоугольном треугольнике BOC:
В прямоугольном треугольнике BOC: 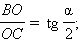
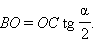 Но
Но
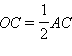 и
и
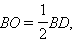 поэтому
поэтому
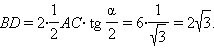
 2 из 6
2 из 6
 |


 Задачи с решениями
Задачи с решениями

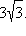 Вычислить длины диагоналей ромба.
Вычислить длины диагоналей ромба.
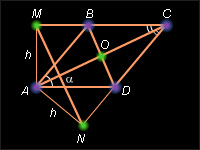
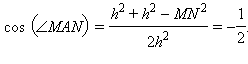 Отсюда
Отсюда ![]() MAC +
MAC + ![]() MCA = 90°
MCA = 90°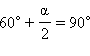 и
и 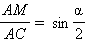 и
и
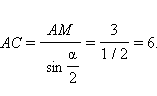 В прямоугольном треугольнике
В прямоугольном треугольнике 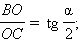
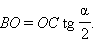 Но
Но
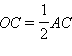 и
и
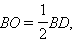 поэтому
поэтому
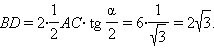
 2 из 6
2 из 6
