Четырехугольник
Задачи с решениями
Из одной точки P проведены секущая PC и касательная PA к окружности, равные соответственно 24 и 12. Найти радиус окружности, если секущая удалена от центра O окружности на 12.
Решение
Шаг 1
На чертеже изображены окружность, касательная и секущая. Пусть касательная пересекает окружность в точке A, а секущая – в точках B и C.
Шаг 2
Известно, что PA2 = PC · PB (следствие 7.3). Значит, 122 = 24 · PB, откуда PB = 6. Теперь находим длину отрезка BC: BC = PC – PB = 24 – 6 = 18.
Шаг 3Точка D – середина хорды BC, поэтому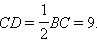 
Шаг 4По теореме Пифагора получаем
OC2 = OD2 + CD2 = 122 + 92 = 225 = 152 и OC = 15.
Ответ: 15.
6 из 6
 |
