Задачи с решениями

Шаг 1

На чертеже изображена данная трапеция ABCD.

Шаг 2

Из точек B и C проведем высоты BE и CF.

Шаг 3

EF = BC = a. Поскольку трапеция равнобедренная, то 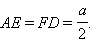  Из прямоугольного треугольника ΔABE находим, что ABE = 30°.

Шаг 4

Пусть точка O – середина отрезка AD, AO = DO = a. Поскольку AO = AB = a и BAO = 60°, то треугольник ΔABO – равносторонний и OB = a. Поскольку трапеция равнобедренная, то OC = OB = a. Таким образом, OA = OB = OC = OD = a.

Шаг 5

Мы видим, что середина отрезка AD – точка O – одинаково удалена ото всех вершин трапеции, и, следовательно, является центром окружности, описанной около трапеции. Значит, радиус этой окружности равен a. Если c – длина окружности, то c = 2πa.

Ответ: c = 2πa.