

 |
 |

Каждый параллелепипед имеет центр симметрии.
Противоположные грани любого параллелепипеда равны и параллельны.

Прямоугольным называется параллелепипед, все грани которого прямоугольники.
Прямоугольный параллелепипед с равными ребрами называется кубом.
Три ребра, выходящие из одной вершины прямоугольного параллелепипеда называются его измерениями (длиной, шириной, высотой).

Квадрат диагонали прямоугольного параллелепипеда равняется сумме квадратов его измерений:
Заметим, что если ребро куба равно 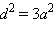 и
и 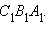
Легко заметить, что все диагонали прямоугольного параллелепипеда равны.
 |
 |
 |

