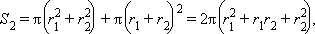Глава 4. Многогранники
4.9. Сечения многогранников
Приведем несколько характерных примеров решения задач на комбинацию многогранников.
Пример 4.1.
Дан куб с ребром a (чертеж 4.9.1). Точки M, N, P – соответственно середины ребер AB, BC, BB1. Найти объем пирамиды D1MNP.
Решение.
Кроме пирамиды D1MNP куб содержит еще четыре пирамиды: PMBN, D1PNCC1B1, D1AMPB1A1, D1AMNCD с объемами соответственно V1, V2, V3, V4. Пирамиды с объемами V2, V3, V4 равновеликие. Пусть V – искомый объем, а Vk – объем куба, тогда V = Vk – 3V2 – V1. Заметим, что
Окончательно имеем
Ответ. 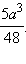
Пример 4.2.
Правильная треугольная призма имеет высоту h и сторону основания a (чертеж 4.9.2). Правильная треугольная пирамида имеет с призмой общее основание и размещена по одну с ней сторону относительно этого основания. Высота пирамиды равна 2h. Найти площадь полной поверхности той части пирамиды, которая лежит внутри призмы.
Решение.
Находим площади оснований:
Пусть Sб – площадь боковой поверхности усеченной пирамиды, тогда Sб = 3S, где S – площадь трапеции ABB2A2. Из Δ POD имеем
тогда
Следовательно,
Ответ. 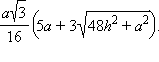
Пример 4.3.
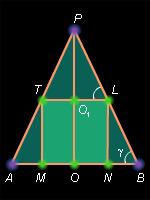
В конус вписан равносторонний цилиндр. Найти объем V цилиндра и площадь Sп его полной поверхности, если образующая конуса составляет с плоскостью его основания угол γ (рис. 4.9.1), а высота конуса равна h.
 1
|
| Рисунок 4.9.1
|
Решение. Осевое сечение данной комбинации – это квадрат MNLT, вписанный в равнобедренный треугольник PAB;  PAB = γ, PO = h – высота конуса; O1 = PO
PAB = γ, PO = h – высота конуса; O1 = PO TL;
TL;  PLT =
PLT =  PBA = γ. Пусть TM = x, тогда
PBA = γ. Пусть TM = x, тогда
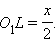 Из Δ PO1L имеем PO1 = O1L tg γ, или
Из Δ PO1L имеем PO1 = O1L tg γ, или
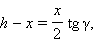 откуда
откуда
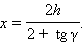 Далее находим
Далее находим
Ответ. 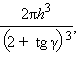
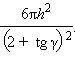
Пример 4.4.
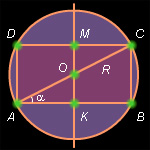
В шар радиуса R (рис. 4.9.2) вписан цилиндр. Отношение площади полной поверхности цилиндра к площади поверхности шара равно t. Какие значения может принимать t?
 2
|
| Рисунок 4.9.2
|
Решение. Осевое сечение данной в условии комбинации шара и цилиндра – прямоугольник ABCD, вписанный в окружность 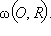 Пусть
Пусть  CAB = α, тогда из Δ AOK имеем OK = R sin α, AK = R cos α. По условию
CAB = α, тогда из Δ AOK имеем OK = R sin α, AK = R cos α. По условию
то есть 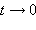 при
при 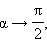 следовательно, t может принимать как угодно малые положительные значения. Для определения максимального значения t найдем производную
следовательно, t может принимать как угодно малые положительные значения. Для определения максимального значения t найдем производную
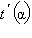 и приравняем ее к нулю:
и приравняем ее к нулю:
откуда 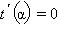 при tg 2α = 2 или при
при tg 2α = 2 или при 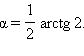 Следовательно,
Следовательно, 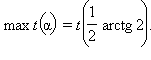 Принимая во внимание, что
Принимая во внимание, что 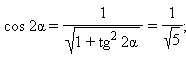
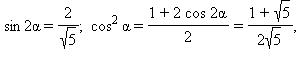 получаем:
получаем:
Ответ. 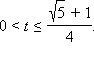
Пример 4.5.
В конус вписан шар радиуса r (рис. 4.9.3). Найти объем конуса, если его высота равна h.
 3
|
| Рисунок 4.9.3
|
Решение. Осевое сечение данной комбинации шара и конуса – это равнобедренный треугольник PAB, описанный вокруг окружности 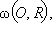 PC = h – высота конуса, OD
PC = h – высота конуса, OD PB.
Объем конуса
PB.
Объем конуса 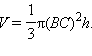 Заметим, что
Заметим, что 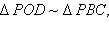 поэтому
поэтому
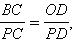 или или 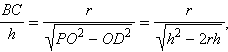 |
откуда 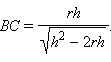 Следовательно, имеем:
Следовательно, имеем: 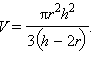
Ответ. 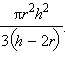
Пример 4.6.
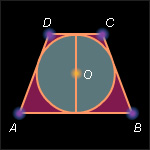
Шар вписан в усеченный конус (рис. 4.9.4). Доказать, что их объемы относятся как площади полных поверхностей.
 4
|
| Рисунок 4.9.4
|
Решение. Осевое сечение шара и усеченного конуса – это равнобедренная трапеция, описанная вокруг окружности 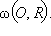 Пусть радиусы оснований усеченного конуса равны r1 и r2, тогда объем шара
Пусть радиусы оснований усеченного конуса равны r1 и r2, тогда объем шара 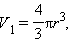 объем усеченного конуса
объем усеченного конуса 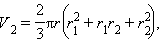
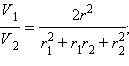 площадь поверхности шара
площадь поверхности шара 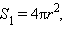 площадь полной поверхности усеченного конуса
площадь полной поверхности усеченного конуса 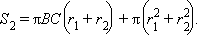 Поскольку
Поскольку 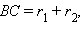 то
то
что и требовалось доказать.






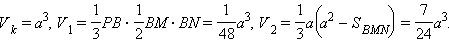
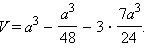
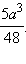
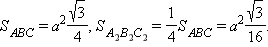
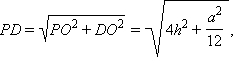
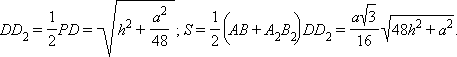
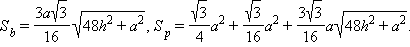
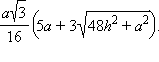

![]() PAB = γ, PO = h
PAB = γ, PO = h![]() TL;
TL; ![]() PLT =
PLT = ![]() PBA = γ
PBA = γ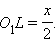 Из
Из 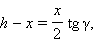 откуда
откуда
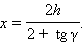 Далее находим
Далее находим
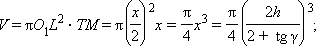
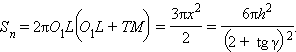
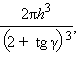
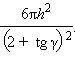

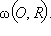 Пусть
Пусть ![]() CAB = α
CAB = α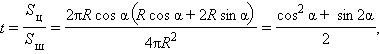
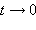 при
при 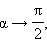 следовательно,
следовательно, 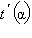 и приравняем ее к нулю:
и приравняем ее к нулю:
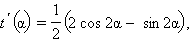
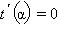 при
при 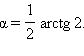 Следовательно,
Следовательно, 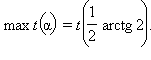 Принимая во внимание, что
Принимая во внимание, что 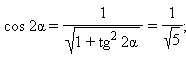
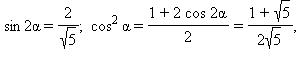 получаем:
получаем:
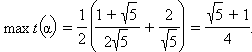
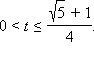

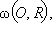
![]() PB
PB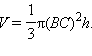 Заметим, что
Заметим, что 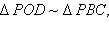 поэтому
поэтому
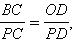 или
или 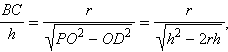
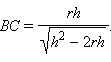 Следовательно, имеем:
Следовательно, имеем: 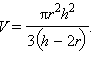
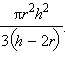

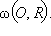 Пусть радиусы оснований усеченного конуса равны
Пусть радиусы оснований усеченного конуса равны 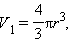 объем усеченного конуса
объем усеченного конуса 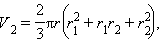
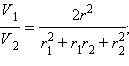 площадь поверхности шара
площадь поверхности шара 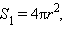 площадь полной поверхности усеченного конуса
площадь полной поверхности усеченного конуса 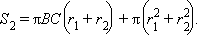 Поскольку
Поскольку 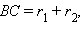 то
то