Многогранники
Задачи с решениями
Основанием пирамиды является равнобедренный треугольник ABC, у которого BC = a, AB = AC = b (см. чертеж). Каждая боковая грань наклонена к плоскости основания под углом γ, и высота проходит внутри пирамиды. Найти:
а) высоту пирамиды;
б) площадь полной поверхности пирамиды.
Решение
Поскольку все боковые грани одинаково наклонены к плоскости основания и высота проходит внутри пирамиды, то основание O высоты – центр окружности, вписанной в ΔABC. Пусть D – середина ребра BC, AD – высота ΔABC.
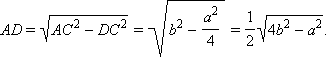DO = r – радиус круга, вписанного в ΔABC.
PDO – линейный угол двугранного угла BC. По условию PDO = γ. Из прямоугольного треугольника PDO имеем
По теореме о площади ортогональной проекции имеем:
SΔABC = Sб cosγ,
тогда
Теперь из равенства (*) имеем:
Ответ: а)
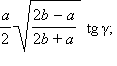
б)
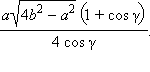
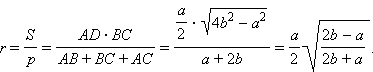
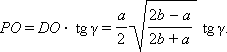
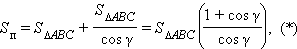
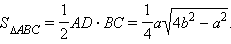
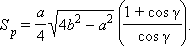
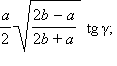
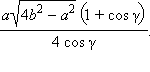
10 из 14
 |
