Многогранники Задачи с решениями
Задачи с решениями

Основанием пирамиды является треугольник со сторонами 6, 8, 10. Каждое боковое ребро равно 13 .
а) Найти высоту пирамиды.
б) Доказать, что одна из боковых граней перпендикулярна плоскости основания.
в) Найти площадь полной поверхности пирамиды.
Решение
Шаг 1
Изобразим данную пирамиду и произведем маркировку рисунка.
Шаг 262 + 82 = 102 или BC2 + AC2 = AB2, значит, ΔABC – прямоугольный,  C = 90°. Все боковые ребра равны, значит, высота пирамиды проходит через центр окружности, описанной около основания. В прямоугольном треугольнике середина гипотенузы – центр описанной окружности.
C = 90°. Все боковые ребра равны, значит, высота пирамиды проходит через центр окружности, описанной около основания. В прямоугольном треугольнике середина гипотенузы – центр описанной окружности.
Шаг 3
Грань PAB содержит высоту PO пирамиды. Поэтому, согласно признаку перпендикулярности двух плоскостей, боковая грань PAB перпендикулярна плоскости основания.
Шаг 4
Площадь Sп полной поверхности пирамиды равна сумме площадей всех ее граней:
Sп = SΔABC + SΔPAB + SΔPBC + SΔPAC. (1)
Шаг 5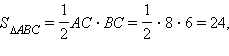
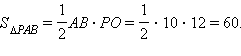
Шаг 6
Найдем площади треугольников PAC и PBC с помощью формулы Герона:
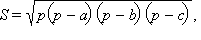 где р – полупериметр треугольника со сторонами a, b, c;
где р – полупериметр треугольника со сторонами a, b, c;
Шаг 7
Теперь из формулы (1) получаем:
Ответ: а) 12, в)
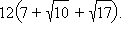
 11 из 14
11 из 14
 |


 Задачи с решениями
Задачи с решениями

 11 из 14
11 из 14
