Тела вращения

Задачи с решениямиЗадачи с решениямиВключить/Выключить фоновую музыкуВключить/Выключить звуки событий


Высота правильной четырехугольной пирамиды равна h (см. чертеж), а плоский угол при вершине пирамиды – α. Найти площадь поверхности шара, описанного вокруг пирамиды.

Решение

По условию PO = h, BPC = α. Пусть PB = b, тогда из ΔPOB имеем

OB2 = PB2 – PO2 = b2 – h2 (*).

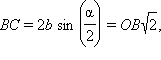Из ΔPBC находим  откуда

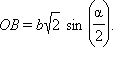
Теперь из равенства (*) имеем

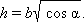
2b2 sin2 (α/2) = b2 – h2, h2 = b2(1 – 2 sin2 (α/2)) = b2 cos α,

По теореме 2 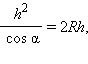b2 = 2Rh, где R – радиус описанного шара, следовательно,  откуда 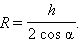Искомая площадь:

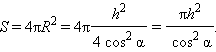
Ответ:

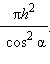
Замечание. В случае, когда пирамида не является правильной, необходимо точно установить положение центра описанного шара.


 12 из 18