Тела вращения Задачи с решениями
Задачи с решениями

В правильной четырехугольной пирамиде центры вписанного и описанного шаров совпадают (см. чертеж). Двугранный угол при ребре основания равен α. Доказать, что cos α = tg (π/8).
Решение
Пусть O' – центр вписанного и описанного шаров правильной четырехугольной пирамиды PABCD, O'E – перпендикуляр, опущенный из точки O' на грань PBC: OO' = O'E = r (радиус вписанного шара). Сечения описанного шара, равноудаленные от его центра, равны. Поэтому квадрат ABCD и треугольник PBC вписаны в равные окружности. Следовательно,  BEC =
BEC =  BOC = π/2 и BPC = π/4.
BOC = π/2 и BPC = π/4.
Проведем апофему PF боковой грани PBC. Поскольку CF = OF, то
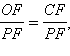 или cos α = tg (π/8), что и требовалось доказать.
или cos α = tg (π/8), что и требовалось доказать.
 14 из 18
14 из 18
 |


 Задачи с решениями
Задачи с решениями

![]() BEC =
BEC = ![]() BOC = π/2
BOC = π/2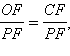 или
или  14 из 18
14 из 18
