Тела вращения Задачи с решениями
Задачи с решениями

Основанием пирамиды является равнобедренный треугольник с боковой стороной b и углом α при вершине (см. чертеж). В эту пирамиду вписан конус, образующая которого составляет с плоскостью основания угол φ. Найти объем пирамиды и площадь ее полной поверхности.
Решение
Высоты конуса и пирамиды совпадают, основанием конуса является круг, вписанный в основание пирамиды. По условию AC = AB = b,  BAC = α. Вписанная окружность касается стороны BC в ее средней точке D (
BAC = α. Вписанная окружность касается стороны BC в ее средней точке D ( PDO = φ – линейный угол двугранного угла BC). Из ΔABD (см. рисунок) имеем
BD = b sin (α/2), AD = b cos (α/2),
PDO = φ – линейный угол двугранного угла BC). Из ΔABD (см. рисунок) имеем
BD = b sin (α/2), AD = b cos (α/2),  ABC = (180° – α)/2 = 90° – α/2.
ABC = (180° – α)/2 = 90° – α/2.
Поскольку BO – биссектриса угла B, то
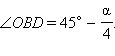 Из ΔOBD имеем
Из ΔOBD имеем
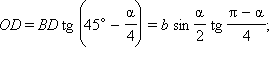
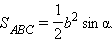 Из ΔPOD (см. первый рисунок) имеем
Из ΔPOD (см. первый рисунок) имеем
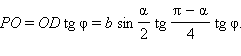
Объем пирамиды
Площадь боковой и полной поверхности
Ответ:
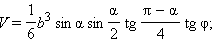
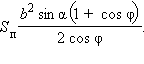
 15 из 18
15 из 18
 |


 Задачи с решениями
Задачи с решениями

![]() BAC = α
BAC = α![]() PDO = φ
PDO = φ![]() ABC = (180° – α)/2 = 90° – α/2
ABC = (180° – α)/2 = 90° – α/2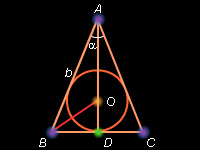
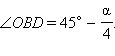 Из
Из 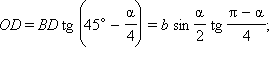
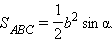 Из
Из 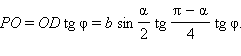
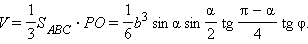
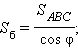
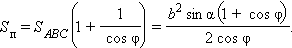
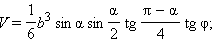
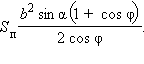
 15 из 18
15 из 18
