Тела вращения Задачи с решениями
Задачи с решениями

Найти площадь сечения шара (x – 3)2 + (y + 2)2 + (z – 1)2 ≤ 25 плоскостью, заданной уравнением 3x – 2y + 4z – 5 = 0.
Решение
Шаг 1
Изобразим сферу с центром O и радиусом R. O1 – центр сечения, отстоящего от центра сферы на расстояние h. Известно, что сечением сферы является окружность, а сечением шара – круг. Прямая OO1 перпендикулярна плоскости сечения. A – любая точка на окружности сечения, поэтому OA = R. Из прямоугольного ΔOO1A находим: O1A2 = R2 – h2. Обозначим через S площадь сечения: S = πO1A2 = π(R2 – h2) (1).
Шаг 2
Пусть дана точка T (x0; y0; z0;) и плоскость с уравнением ax + by + cz + d = 0. Обозначим расстояние от точки до указанной плоскости через h. Согласно формуле расстояния от точки до плоскости (смотри об этом в главе 8),
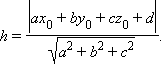
Шаг 3
Находим расстояние h от центра шара O (3; –2; 1) до плоскости с уравнением 3x – 2y + 4z – 5 = 0: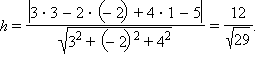
Шаг 4
Пользуясь формулой (1), получаем:
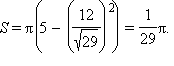 (Мы учли, что радиус шара равен 5).
(Мы учли, что радиус шара равен 5).
Ответ:
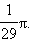
 9 из 18
9 из 18
 |


 Задачи с решениями
Задачи с решениями

 9 из 18
9 из 18
