Задачи с решениями

Касательная плоскость образует с плоскостью осевого сечения цилиндра угол 30°. Найти минимальное расстояние между диагональю этого осевого сечения и образующей, через которую проходит касательная плоскость, если радиус цилиндра равен R.

Отрезок T₁T лежит на линии пересечения плоскости ABB₁A₁ осевого сечения и касательной плоскости (см. рисунок), проходящей через образующую M₁M; B₁T₁M₁ = 30°. Прямые AB₁ и M₁M скрещивающиеся. Плоскость ABB₁A₁ содержит прямую AB₁ и параллельна прямой M₁M. Поэтому искомое расстояние равно расстоянию от прямой M₁M до плоскости ABB₁A₁. Опустим теперь перпендикуляр M₁K₁ из точки M₁ на прямую A₁B₁; O₁M₁T₁ = 90°, т.к. M₁T₁ – касательная к окружности верхнего основания цилиндра; B₁O₁M₁ = 60°. Из прямоугольного треугольника O₁M₁K₁ имеем:

Ответ:

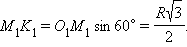
10 из 18