Объемы многогранников Задачи с решениями
Задачи с решениями

Основанием пирамиды является правильный треугольник со стороной a, одна из боковых граней перпендикулярна плоскости основания, а две другие образуют с плоскостью основания угол γ. Найти объем пирамиды.
Решение
Шаг 1
Изображаем данную пирамиду и маркируем рисунок. По условию AB = BC = CA = a. Грань PAB перпендикулярна плоскости основания. Поэтому высота PO пирамиды лежит в грани PAB. Возникает вопрос: где находится данный угол γ?
Шаг 3
Известно, что объем пирамиды V находится по формуле:
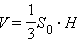 (1), где S0 – площадь основания, H – высота пирамиды.
(1), где S0 – площадь основания, H – высота пирамиды.
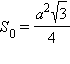 – площадь правильного треугольника со стороной a. Остается найти высоту.
– площадь правильного треугольника со стороной a. Остается найти высоту.
Шаг 4
Треугольники POK и POM равны, как прямоугольные треугольники с общим катетом PO и равными острыми углами. Значит, OK = OM. Легко видеть, что треугольники BOK и AOM равны, а значит,
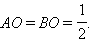
Шаг 5
Из прямоугольного треугольника POK имеем: H = PO = OK·tg γ (2).
Поскольку O – середина стороны AB, то OK – средняя линия ΔABD. Значит,
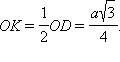
Из формулы (2) получаем:
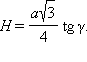
Шаг 6
Теперь из формулы (1) имеем:
Ответ: 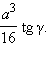
 7 из 8
7 из 8
 |


 Задачи с решениями
Задачи с решениями

 7 из 8
7 из 8
