Объемы многогранников Задачи с решениями
Задачи с решениями

Все грани параллелепипеда – равные между собой ромбы со стороной a и острым углом α. Найти объем параллелепипеда.
Решение
Шаг 1
Изображаем на рисунке данный параллелепипед и маркируем рисунок. Заметим, что все ребра параллелепипеда имеют одинаковою длину a.
Шаг 2
Известно, что объем параллелепипеда находится по формуле V = S0·H (1), где S0 – площадь основания, H – высота параллелепипеда. Зная формулу площади ромба, находим: S0 = a2sinα. Осталось найти высоту параллелепипеда. Однако неясно, как искать высоту. Если мы проведем из точки B1 перпендикуляр B1O на плоскость основания, то где лежит точка O?
Шаг 3
Пусть в некоторой плоскости α лежит угол M. Прямая a не лежит в плоскости α, проходит через точку M и образует со сторонами угла M равные углы. Тогда проекцией прямой a на плоскость α является биссектриса угла M. Пусть O = ПрαA, A – произвольная точка прямой a. Проведем из точки O перпендикуляры OB и OC на стороны угла M. По теореме о трех перпендикулярах AB MB, и AC
MB, и AC MC. Треугольники AMB и AMC равны (у них общая гипотенуза и равные острые углы: по условию
MC. Треугольники AMB и AMC равны (у них общая гипотенуза и равные острые углы: по условию  AMB =
AMB =  AMC). Отсюда следует, что AB = AC. Далее видим, что OB = OC, т. к. равные наклонные AB и AC, проведенные из одной точки, имеют равные проекции. Из равенства OB = OC следует, что
AMC). Отсюда следует, что AB = AC. Далее видим, что OB = OC, т. к. равные наклонные AB и AC, проведенные из одной точки, имеют равные проекции. Из равенства OB = OC следует, что  OMB =
OMB =  OMC, т. е. MO – биссектриса угла M.
OMC, т. е. MO – биссектриса угла M.
Шаг 4
Проведем высоту параллелепипеда B1O. Поскольку  B1BC =
B1BC =  B1BA, то согласно результату, полученному на третьем шаге, точка O лежит на биссектрисе угла ABC, т. е. на диагонали BD.
B1BA, то согласно результату, полученному на третьем шаге, точка O лежит на биссектрисе угла ABC, т. е. на диагонали BD.
Шаг 6
Из прямоугольного ΔB1BO имеем:
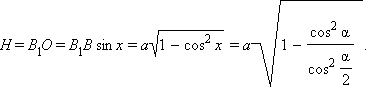 Подставив полученный результат в формулу (1), имеем:
Подставив полученный результат в формулу (1), имеем:
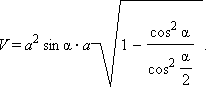
Ответ: 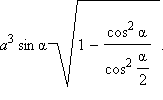
Замечание. Можно (но не обязательно) преобразовать полученный ответ:
Поэтому
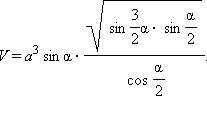
 6 из 8
6 из 8
 |


 Задачи с решениями
Задачи с решениями

 6 из 8
6 из 8
