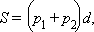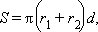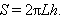1

Рисунок 7.5.1

Доказательство этого факта получается непосредственно из формулы площади трапеции, поскольку рассматриваемая часть боковой поверхности состоит из равных трапеций.

2

Рисунок 7.5.2

Доказываемая формула получается из предыдущей предельным переходом аналогично тому, как мы получали формулу объема конуса из формулы объема пирамиды.

Поверхность, которая получится при вращении такого отрезка, очевидно, представляет собой часть боковой поверхности конуса, которую мы рассматривали в Лемме 7.2.

3

Рисунок 7.5.3

Пусть A₁ и B₁ – проекции A и B на m, N – середина AB, MN – отрезок серединного перпендикуляра к AB. Точка M расположена на прямой m; N₁ – проекция N на m; B₂ – проекция A на BB₁. Согласно обозначениям, введенным в условии теоремы, A₁B₁ = AB₂ = h, MN = L, NN₁ равна средней линии трапеции AA₁B₁B, AA₁ + BB₁ = ₂NN₁. Согласно предыдущей лемме имеем

S = π · (AA1 + BB1) · AB = 2π · AB · NN1.

Треугольники и подобны, откуда получаем, что откуда Итак, имеем

S = 2πAB2 · NM = 2πLh,

что и требовалось доказать.

4

Рисунок 7.5.4

Рассмотрим в данной сфере диаметр PQ, перпендикулярный плоскостям, ограничивающим данный сферический пояс, и возьмем сечение сферы плоскостью, проходящей через PQ. Тогда сечением сферического пояса будут две дуги, симметричные относительно PQ. Длина проекции каждой из этих дуг на PQ равна h. Сам же сферический пояс получается в результате вращения какой-либо из этих дуг, например, CD, вокруг прямой PQ.

Разобьем дугу CD на n равных частей и соединим их последовательно друг за другом. Получится равнозвенная ломаная, вписанная в эту дугу. Пусть O – центр сферы. Пусть также L_n – расстояние от центра сферы до звеньев ломаной; так как все звенья равны, то они все равноудалены от центра сферы. При вращении ломаной вокруг PQ получим поверхность, составленную из частей конических поверхностей. Применим теперь к каждой части формулу предыдущей леммы и сложим найденные значения. Тогда для площади поверхности, образовавшейся в результате вращения ломаной, справедлива формула

Очевидно, что с возрастанием n величина L_n стремится к R. Принимая за площадь поверхности сферического пояса величину, к которой стремится S_n, получим искомую формулу.

Отметим, что полученная формула действительно дает правильное значение площади поверхности сферического пояса, поскольку с ростом числа звеньев ломаной, вписанной в нашу дугу окружности, касательные плоскости к поверхности, возникающей в результате вращения этой ломаной, приближаются к касательным плоскостям сферического пояса.

Отметим также, что по этой же самой формуле может быть найдена площадь поверхности сферического сегмента. Этот случай отвечает той ситуации, когда одна из плоскостей касается сферы. Если же в полученной формуле положить h = 2R (обе плоскости касаются сферы), то получим, как и ожидалось, формулу площади сферы S_сф = 4πR².