Объемы и поверхности круглых тел
Задачи с решениями
Два равных шара радиуса R размещены так, что центр каждого из них лежит на поверхности другого. Найти объем общей части шаров.
Решение
Шаг 1
Изображаем осевое сечение данных шаров с центрами O1 и O2 и радиусами R и маркируем рисунок. Мы видим на рисунке большие круги данных шаров, которые пересекаются, причем центр каждого круга лежит на окружности другого. Общая часть данных шаров – это два шаровых сегмента с общим основанием. Попытаемся найти объем одного такого шарового сегмента.
Шаг 2
Известно, что объем V шарового сегмента находится по формуле
где
R – радиус шара,
h – высота шарового сегмента.
Шаг 3
Вернемся к рисунку. O1O2 – линия центров окружностей. Поэтому треугольник O1AO2 – равносторонний. AO1 = O1O2 = O2A = R. B – середина отрезка O1O2. O1B – высота указанного шарового сегмента.
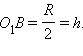
Шаг 4
Подставляем найденное значение в формулу (1):
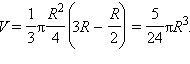Для того чтобы найти объем общей части шаров, надо этот результат удвоить.
Ответ: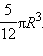 
7 из 8
 |
(1),
