Рассмотрим октаэдр ABCDEG с ребром 1 (чертеж 8.3.1). Выберем точки M, K, N, Q, L и P на его ребрах AE, BE, CE, DE, AB и BC соответственно так, чтобы AM = EK = CN = EQ = BL = BP = x. Выберем x таким, чтобы все отрезки, соединяющие эти точки, были равны между собой.

Чертеж 8.3.1

Очевидно, что для этого достаточно выполнения равенства KM = KQ. Однако, поскольку KEQ – равнобедренный прямоугольный треугольник с катетами KE и EQ, то 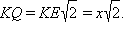Запишем теорему косинусов для треугольника MEK, в котором ME = 1 – x, KE = x, MEK = 60°:

Отсюда 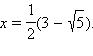Второй корень, который больше 1, не подходит. Выбрав x таким образом, построим искомый многогранник. Выберем еще шесть точек, симметричных точкам K, L, P, N, Q и M относительно центра тетраэдра, и обозначим их K₁, L₁, P₁, N₁, Q₁ и M₁ соответственно. Полученный многогранник с вершинами K, L, P, N, Q, M, K₁, L₁, P₁, N₁, Q₁ и M₁ и есть искомый. У него все грани – правильные треугольники, из каждой вершины выходит пять ребер. Докажем теперь, что все его двугранные углы равны между собой.

Для этого заметим, что все вершины построенного двадцатигранника равноудалены от точки O – центра октаэдра, то есть расположены на поверхности сферы с центром O. Далее поступим так же, как и при доказательстве существования правильного октаэдра. Соединим все вершины двадцатигранника с точкой O. Совершенно аналогично докажем равенство треугольных пирамид, основания которых – грани построенного многогранника, и убедимся, что все двугранные углы двадцатигранника вдвое больше углов при основании этих равных треугольных пирамид. Следовательно, все двугранные углы равны, а значит, полученный многогранник – правильный. Он и называется икосаэдром.

Как видно, количество граней и вершин многогранника, существование которого мы сейчас стараемся доказать, равно числу вершин и граней икосаэдра. Таким образом, если мы докажем существование многогранника, о котором идет речь в этой теореме, то он непременно окажется двойственным к икосаэдру. На примере куба и октаэдра мы видели, что двойственные фигуры обладают тем свойством, что вершины одной из них лежат в центрах граней другой. Это наводит на идею доказательства данной теоремы.

1

Рисунок 8.3.1

Возьмем икосаэдр и рассмотрим многогранник с вершинами в центрах его граней (чертеж 8.3.2). Очевидно, что центры пяти граней икосаэдра, имеющих общую вершину, лежат в одной плоскости и служат вершинами правильного пятиугольника (в этом можно убедиться способом, аналогичным тому, что мы применяли при доказательстве леммы 8.1). Итак, каждой вершине икосаэдра соответствует грань нового многогранника, грани которого – правильные пятиугольники, а все двугранные углы равны. Это следует из того, что любые три ребра, выходящие из одной вершины нового многогранника, можно рассматривать, как боковые ребра правильной треугольной пирамиды, и все получающиеся при этом пирамиды равны (у них равны боковые ребра и плоские углы между ними, которые суть углы правильного пятиугольника). Из всего вышесказанного следует, что полученный многогранник является правильным и имеет 12 граней, 30 ребер и 20 вершин. Такой многогранник и называется додекаэдром.