|
|
Векторы называются компланарными, если имеются равные им вектора, параллельные одной плоскости.
Любые два вектора компланарны. Любые три вектора, среди которых есть два коллинеарных, компланарны.
|
| Рисунок 9.2.1 |
На рисунке 9.2.1 векторы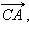 
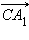и 
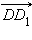компланарны, так как, если отложить от точки 
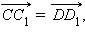то все три вектора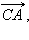 
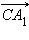и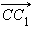 
окажутся лежащими в одной плоскости. Векторы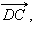 
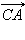и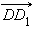 
не компланарны, так как вектор 
не лежит в плоскости
Пусть векторы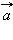 
и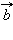 
не коллинеарны, тогда для любого вектора 
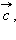лежащего в одной плоскости с 
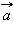и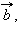 
существует единственная пара чисел α и β, такая, что
 |
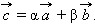Эта теорема верна и для того случая, когда векторы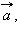 
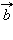и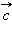 
параллельны одной плоскости.
Если векторы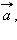 
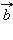и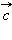 
,
отложенные от одной точки, не лежат в одной плоскости, то равенство
 |
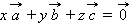Эта теорема позволяет от одного векторного равенства переходить к системе числовых равенств.
Любой вектор можно разложить по трем данным некомпланарным векторам, причем коэффициенты разложения определяются единственным образом.
Эта теорема доказывается аналогично теореме 9.4, и поэтому мы не будем на ней подробно останавливаться.
|
|
 |
и 
Спроектируем конец вектора 
на прямые, задаваемые векторами 
и 
в направлении, параллельном другому вектору (рис. 9.2.2). Обозначим вектора с началами в точке 
и 
Так как эти вектора лежат на тех же прямых, что и 
,
и 
то по 
При этом по 
Значит, 
по векторам 
и 
то есть нашлись две пары чисел 
и 
таких, что 
и справедливы разложения: 
и 
Вычитая из первого равенства второе, получаем 
Отсюда, ввиду того что 
следует,
что 
то есть 
что по условию не так. Полученное противоречие означает, что неравенство 
невозможно, а значит 
Аналогично доказывается, что 
Теорема доказана.
следует, что 
Значит, вектор 
лежит в одной плоскости с векторами 
и 
что неверно. Поэтому