

 |
 |
Рассмотрим три взаимно перпендикулярные прямые
|
|
|
| Чертеж 9.3.1. Декартовы координаты в пространстве
|
Проведем через каждую пару этих прямых плоскость. Плоскость, проходящая через прямые

Прямые
Рассмотрим теперь произвольную точку
|
|
|
| Чертеж 9.3.2. Координаты точки
|
Пусть эта плоскость пересекает ось

Координатой точки
Если же точка
Зададим теперь в пространстве прямоугольную систему координат.

Единичным вектором или ортом называется вектор, длина которого равна единице и который направлен вдоль какой-либо координатной оси. Единичный вектор, направленный вдоль оси 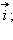 единичный вектор, направленный вдоль оси
единичный вектор, направленный вдоль оси 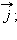 вдоль оси
вдоль оси 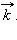 Вектора
Вектора 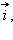
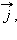
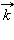 называются координатными векторами.
называются координатными векторами.
По своему построению эти векторы некомпланарны, а значит, любой вектор 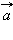 можно разложить по координатным векторам:
можно разложить по координатным векторам:
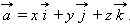 |
Кроме того, отметим, что по уже доказанному коэффициенты разложения определяются единственным образом. Эти коэффициенты и называются координатами вектора 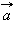 в данной системе координат.
в данной системе координат.
Следующие утверждения доказываются аналогично их планиметрическим аналогам.
Координаты нулевого вектора равны нулю.
Координаты равных векторов соответственно равны.
Пусть 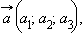
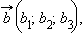 тогда
тогда 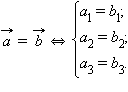
Координаты вектора суммы двух векторов равны сумме соответствующих координат этих векторов.
Пусть 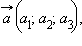
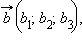 тогда
тогда 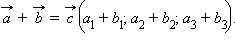
Координаты вектора разности двух векторов равны разностям соответствующих координат этих векторов.
Пусть 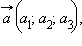
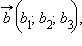 тогда
тогда 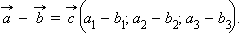
Координаты вектора произведения данного вектора на число равны произведениям соответствующих координат этого вектора на данное число.
Пусть 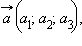
 тогда
тогда 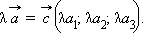
 |
 |
 |

