Глава 1. Арифметика
1.1.
1.1.4.
Система счисления – это совокупность приёмов и правил для записи чисел цифровыми знаками. Системы счисления делятся на позиционные и непозиционные. Позиционной называется система счисления, в которой используется определённое число знаков для обозначения чисел, но значение каждого символа зависит от того, как этот символ расположен по отношению к другим символам в том же числе. Непозиционной называется система счисления, в которой используется определённое число знаков для обозначения чисел, но значение каждого символа не зависит от того, как этот символ расположен по отношению к другим символам в том же числе, и всегда одно и то же.
В процессе развития человеческой цивилизации люди использовали различные системы счисления, однако самой удобной для практических нужд оказалась десятичная система счисления. Разумеется, во многом это было связано с физиологическими особенностями человеческого тела; в самом деле, ведь у человека на руках десять пальцев. Конечно же, не нужно думать, что другие системы счисления совсем не используются. Например, для различных машинных вычислений необыкновенно эффективны вычисления в двоичной системе счисления. Познакомимся же с принципом записи числа в позиционной системе счисления.
 1 1
|
| Рисунок 1.1.4.1. В разное время арабские цифры выглядели по-разному
|
В частности, десятичная система счисления основана на представлении чисел в виде:
|
|
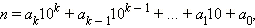 |
(2)
|
где a0, a1, ..., ak – числа от 0 до 9, причём ak ≠ 0. Если справедливо последнее соотношение, то число n записывают коротко так:
или просто
Две последние записи обозначают одно и тоже и применяются одинаково часто.
Для того, чтобы перевести число, записанное в q-ичной системе счисления, в десятичную систему счисления, нужно просто провести все вычисления в формуле (1). Для того, чтобы перевести число из десятичной системы счисления в q-ичную, можно попытаться представить его в виде (1).
Пример 1Записать число 132 в 1) троичной; 2) пятеричной; 3) семеричной; 4) двенадцатеричной.
- 132 = 81 + 27 + 2 ∙ 9 + 2 ∙ 3 = 1 ∙ 34 + 1 ∙ 33 + 2 ∙ 32 + 2 ∙ 31 + 0 = (11220)3.
- 132 = 1 ∙ 53 + 0 ∙ 52 + 1 ∙ 5 + 2 = (1012)5.
- 132 = 2 ∙ 72 + 4 ∙ 7 + 6 = (246)7.
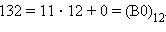
В том случае, если основание системы больше 10, в качестве «дополнительных цифр» используются буквы.
Так, буква B последнем примере обозначает цифру «11» в двенадцатеричной системе счисления.
Ответ. 1) (11220)3, 2) (1012)5, 3) (246)7, 4) (B0)12
|
Для того чтобы перевести число, записанное в десятичной системе, в любую q-ичную систему счисления, можно использовать следующее наблюдение. Перепишем формулу (1) в виде:
Отсюда следует, что 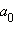 есть остаток от деления числа n на q. Совершенно аналогично,
есть остаток от деления числа n на q. Совершенно аналогично, 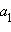 есть остаток от деления числа
есть остаток от деления числа 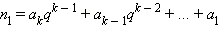 на q. Понятно, что так можно найти все числа ak.
на q. Понятно, что так можно найти все числа ak.
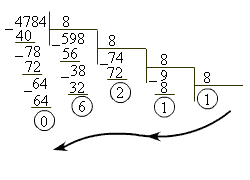
Пример 2Записать число 4784 в восьмеричной системе счисления.
 2 2
|
| Рисунок 1.1.4.2. Перевод числа 4784 в восьмеричную систему счисления |
Ответ. 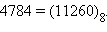 |







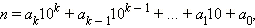
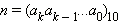
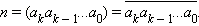
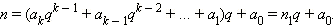
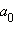 есть остаток от деления числа
есть остаток от деления числа 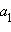 есть остаток от деления числа
есть остаток от деления числа 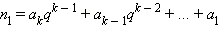 на
на 



