Глава 1. Арифметика

1.1.

Назад Вперед
Назад Вперед

1.1.5.

Теперь, когда у нас уже определены положение натуральных чисел на координатной прямой и число 0, мы можем расширить числовое множество так, чтобы операция вычитания была определена на всем множестве.

1
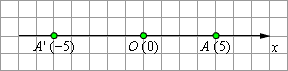Рисунок 1.1.5.1

Рассмотрим снова координатную прямую x. Заметим, что единичный отрезок можно откладывать на этой прямой не только вправо от точки O, обозначая тем самым натуральные числа, но и влево. Рассмотрим, например, точку A, как было сказано выше, отвечающую числу 5. Построим теперь точку A', симметричную точке A относительно точки O. Координатой точки A считается число 5, а координату точки A' записывают так: –5 и читают «минус пять». По определению, координатой точки O считается число 0 (нуль). Числа 5 и –5 называют числами противоположными. Аналогично, любому натуральному числу соответствует противоположное.

 

Множество всех чисел, противоположных натуральным, называется множеством целых отрицательных чисел. Сами натуральные числа при этом называют целыми положительными числами. Множество целых отрицательных чисел, множество целых положительных чисел и число нуль вместе называются множеством целых чисел.

Это множество обозначается 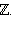Сами натуральные числа иногда записывают со знаком плюс (+), а им противоположные всегда пишут со знаком минус (–). Знак минус перед целым отрицательным числом называется знаком количества в отличие от знака вычитания, который называется знаком действия.

Заданное направление координатной прямой называется положительным, противоположное направление называется отрицательным.

 

 

Модулем (абсолютной величиной) числа называется:

  • само число, если оно положительное,
  • 0, если число равно 0,
  • противоположное положительное число, если число – отрицательное.

В нашем примере модулем числа –5 является число 5. Операция модуль обозначается двумя вертикальными чертами, например,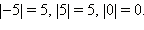

Мы помним, что разность двух натуральных чисел не всегда является натуральным числом. Теперь, введя множество отрицательных чисел, мы можем изучить операции на множестве целых чисел.

Сложение.

  1. Для того, чтобы сложить два целых числа с одинаковыми знаками, нужно сложить их модули и перед суммой поставить их общий знак.

    Пример 1

    Вычислите (+2) + (+5).

    Показать решение

    Пример 2

    Вычислите (–4) + (–7).

    Показать решение

  2. Для того, чтобы сложить два целых числа с разными знаками, нужно из модуля большего числа вычесть модуль меньшего и перед результатом поставить знак большего по модулю числа.

    Пример 3

    Вычислите (–2) + (+5).

    Показать решение

    Пример 4

    Вычислите (+4) + (–7).

    Показать решение

Вычитание.

Вычитание двух целых чисел сводится к сложению уменьшаемого и числа, противоположному вычитаемому.

Умножение.

Для того, чтобы перемножить два целых числа, нужно перемножить их модули и перед произведением поставить знак плюс (+), если исходные числа были одного знака, и минус (–) – если разного.

Правило знаков при умножении:

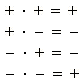При перемножении нескольких сомножителей знак произведения положителен, если число отрицательных сомножителей чётно, и отрицателен, если нечётно.

Деление.

Для того, чтобы разделить одно целое число на другое, нужно разделить модуль первого числа на модуль второго и поставить перед частным знак плюс, если знаки делимого и делителя одинаковые, и минус, – если разные.


Назад Вперед
Наверх

Включить/Выключить фоновую музыкуВключить/Выключить звуки событий