

 |
 |
Оказывается, что для нужд самой математики как, впрочем, и для практики, уже введённых рациональных чисел не хватает. Исторически числа, отличные по своей природе от рациональных, впервые появились уже при желании вычислить диагональ квадрата по его стороне.
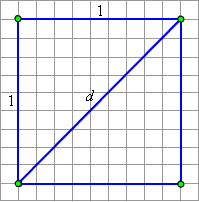 |
| Рисунок 1.3.1.1 |
Покажем, что длина такой диагонали не может быть выражена рациональным числом. Рассмотрим квадрат со стороной, равной 1. Пусть длина его диагонали равна  то есть
то есть 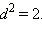 Предположим, что
Предположим, что 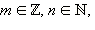 что
что 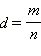 и дробь
и дробь 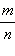 несократима. Получаем:
несократима. Получаем: 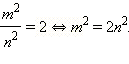 Из этого равенства следует, что, так как правая его часть делится на 2, то и его левая часть делится на 2. Значит и число
Из этого равенства следует, что, так как правая его часть делится на 2, то и его левая часть делится на 2. Значит и число 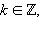 что
что 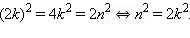 Однако из последнего равенства аналогично следует, что число
Однако из последнего равенства аналогично следует, что число 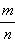 несократима). Значит, не существует такого рационального числа, которое бы выражало длину диагонали квадрата.
несократима). Значит, не существует такого рационального числа, которое бы выражало длину диагонали квадрата.
 |
 |
|
 |
 |
|
Из нашего примера следует, что такие числа существуют: длина диагонали квадрата со стороной 1 является именно таким числом. Аналогично можно доказать, что не существует рационального числа, квадрат которого равен 5, 7, 10, то есть числа 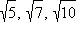 являются иррациональными. Теперь вспомним, что любое рациональное число может быть представлено в виде периодической десятичной дроби и наоборот, любая десятичная периодическая дробь может быть представлена в виде рационального числа.
являются иррациональными. Теперь вспомним, что любое рациональное число может быть представлено в виде периодической десятичной дроби и наоборот, любая десятичная периодическая дробь может быть представлена в виде рационального числа.
Любое иррациональное число можно записать в виде бесконечной непериодической дроби, и любая непериодическая дробь является иррациональным числом. |
 |
 |
|
 |
 |
|
Каждому действительному числу отвечает точка на координатной прямой, и наоборот, каждая точка на координатной прямой соответствует действительному числу. Действительно, для любой точки координатной прямой достаточно найти расстояние до неё от начала координат, а потом поставить перед этим числом знак плюс (+), если точка располагается правее начала координат, и знак минус (–) – если левее.
Изученные множества чисел обозначаются следующим образом:
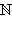 – множество натуральных чисел;
– множество натуральных чисел;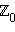 – множество неотрицательных целых чисел (расширенный ряд натуральных чисел);
– множество неотрицательных целых чисел (расширенный ряд натуральных чисел);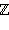 – множество целых чисел;
– множество целых чисел;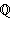 – множество рациональных чисел;
– множество рациональных чисел;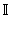 – множество иррациональных чисел;
– множество иррациональных чисел;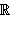 – множество действительных чисел.
– множество действительных чисел.Множество целых чисел
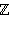 содержится во множестве рациональных чисел
содержится во множестве рациональных чисел
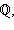 которое, в свою очередь, является частью всего множества действительных чисел
которое, в свою очередь, является частью всего множества действительных чисел 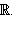 Эти отношения можно записать кратко в виде
Эти отношения можно записать кратко в виде 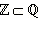 ,
,
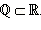
Совершенно аналогично десятичным дробям вводятся правила действия над действительными числами.
Сложение. Сумма двух действительных чисел одного знака есть число того же знака. Модуль такой суммы равен сумме модулей слагаемых.
Сумма двух действительных чисел разных знаков имеет тот же знак, что и большее по модулю слагаемое. Модуль суммы равен разности модулей большего и меньшего слагаемых.
Вычитание. Чтобы вычесть из одного действительного числа другое действительное число, нужно к уменьшаемому прибавить число, противоположное вычитаемому.
Умножение и деление. Произведение (частное) двух действительных чисел одного знака есть число положительное. Произведение (частное) двух действительных чисел разных знаков есть число отрицательное. Модуль произведения (частного) двух действительных чисел равен произведению (частному) модулей этих чисел.
Арифметические операции над действительными числами обладают следующими свойствами (основные законы алгебры).
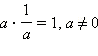 (существование обратного числа).
(существование обратного числа).Сравнение действительных чисел производится совершенно аналогично сравнению рациональных чисел. А именно, говорят, что действительное число
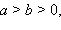 то
то 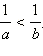
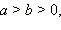 то для любого натурального числа
то для любого натурального числа 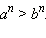
 |
 |
|
 |
 |
|
Кратко:
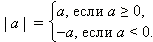 |
 |
 |
 |

