

 |
 |
Для того чтобы найти некоторую часть числа, нужно это число умножить на дробь, выражающую эту часть.
Пусть задана величина некоторой части числа. Чтобы найти само число, нужно величину этой части разделить на дробь, выражающую эту часть.
 |
 |
|
 |
 |
|
Записывается это так: запись 1 % означает 0,01; 75 % означает 0,75; 100 % означает 1; 235 % означает 2,35.

 |
|
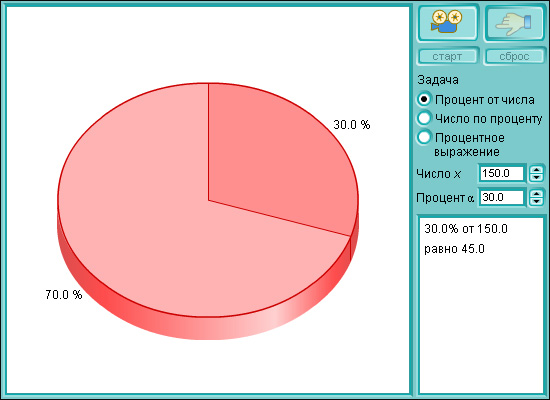
Модель 1.12.
Вычисление процентов
|
Если нам задана часть числа в виде десятичной дроби, то процентное выражение данной десятичной дроби можно найти, умножив её на 100. То же самое получится, если перенести запятую в этой дроби на два разряда вправо. Например, процентное выражение числа 0,1415 есть 14,15 %, числа 2,625 есть 262,5 % и т. д.
Если же дано само процентное выражение числа, то это число можно найти, разделив процентное выражение на 100. Опять же, то же самое получится, если перенести запятую в процентном выражении на два разряда влево. Например, 12,14 % = 0,1214, 325,75 % = 3,2575 и т. д.
Традиционно существует три основные задачи на проценты.
Найти известный процент данного числа. Для решения этой задачи нужно данное число умножить на дробь, выражающую указанный процент.
Найти число по данной величине его указанного процента. Для того чтобы решить эту задачу, нужно данную величину разделить на дробь, выражающую указанный процент.
Найти число 1) 25 % которого составляют 34; 2) 156 % которого составляют 21,84.
Найти выражение одного числа в процентах от другого. Для того чтобы решить эту задачу, нужно данную величину умножить на 100 и результат разделить на второе число.
 |
 |
|
 |
 |
|
Из свойств обыкновенных дробей следует, что справедливы следующие утверждения:
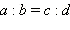 можно записать в виде
можно записать в виде 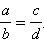
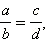 то
то 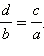
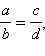 то
то 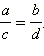
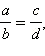 то
то 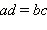 (основное свойство пропорции).
(основное свойство пропорции).
 |
 |
 |

