Глава 2. Алгебраические выражения
2.2.
2.2.5.
В § 2.2.4 мы определили значение выражения ax для всех a > 0 и всех x. Если a = 1, то ax = 1 при всех x. Следовательно, при a > 0, a ≠ 1, определена функция y = ax, отличная от постоянной. Эта функция называется показательной функцией с основанием a.
К основным свойствам показательной функции y = ax при a > 1 относятся:
- Область определения функции − вся числовая прямая.
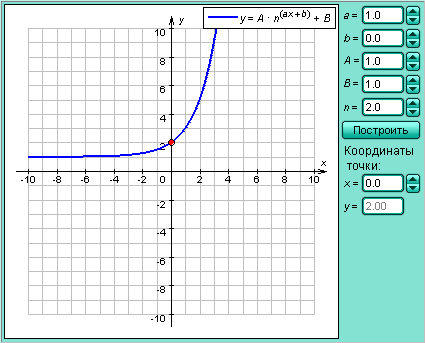
- Область значений функции − промежуток
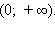
- Функция строго монотонно возрастает на всей числовой прямой, то есть, если
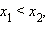 то
то 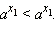
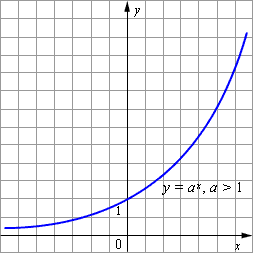
- График показательной функции с основанием a > 1 изображён на рисунке.
 1 1
|
| Рисунок 2.2.5.1. Функция y = ax при a > 1 |
 2 2
|
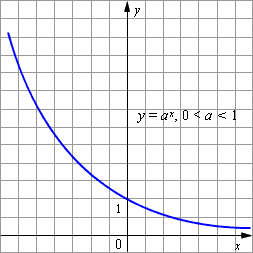
| Рисунок 2.2.5.2. Функция y = ax при 0 < a < 1 |
К основным свойствам показательной функции y = ax при 0 < a < 1 относятся:
- Область определения функции − вся числовая прямая.
- Область значений функции − промежуток
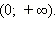
- Функция строго монотонно убывает на всей числовой прямой, то есть, если
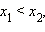 то
то 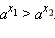
- График показательной функции с основанием 0 < a < 1 изображён на рисунке.
К общим свойствам показательной функции как при 0 < a < 1, так и при a > 1 относятся:
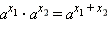 для всех
для всех 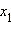 и
и 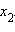
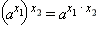 для всех
для всех 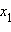 и
и 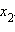
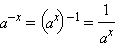 для любого x.
для любого x.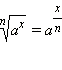 для любого x и любого
для любого x и любого 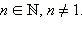
- (ab)x = axbx для любых a, b > 0, a, b ≠ 1.
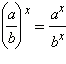 для любых a, b > 0, a, b ≠ 1.
для любых a, b > 0, a, b ≠ 1.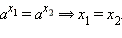
Все эти свойства следуют из свойств операции возведения в степень. Третье и четвёртое свойства являются непосредственным следствием второго. Седьмое свойство следует из строгой монотонности показательной функции и даёт способ решения простейших показательных уравнений.
Пример 1Упростите выражение 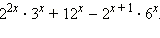
Имеем 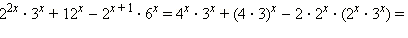
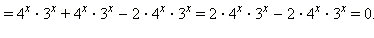
Ответ. 0.
|
Пример 2Решите уравнение: 1) 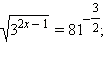 2)
2) 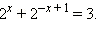

 |
|
Модель 2.4.
Показательная функция
|






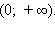
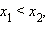 то
то 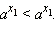


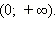
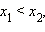 то
то 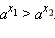
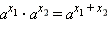 для всех
для всех 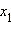 и
и 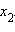
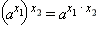 для всех
для всех 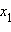 и
и 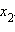
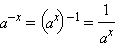 для любого
для любого 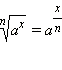 для любого
для любого 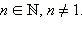
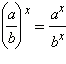 для любых
для любых