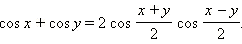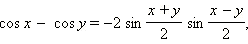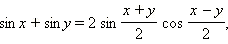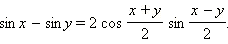Глава 2. Алгебраические выражения
2.4.
2.4.2.
Формулы приведенияПрежде всего, получим формулы, по которым тригонометрические функции углов вида 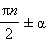 можно выражать через тригонометрические функции угла α. Эти формулы называются формулами приведения.
можно выражать через тригонометрические функции угла α. Эти формулы называются формулами приведения.
 1 1
|
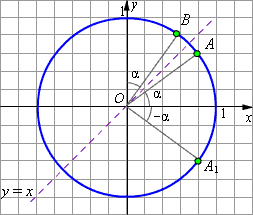
| Рисунок 2.4.2.1
|
Отложим от положительного направления оси абсцисс угол α (см. рис. 2.4.2.1). Отразим точку A, отвечающую этому углу, относительно прямой y = x. Пусть она при отражении перейдёт в точку B. Так как координатные оси тоже симметричны относительно прямой y = x, то угол между осью ординат и радиус-вектором 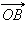 равен α.
равен α.
Несложно сообразить, что угол между положительным направлением оси абсцисс и радиус-вектором 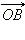 равен
равен 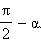 Пусть координаты радиус-вектора
Пусть координаты радиус-вектора 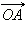 будут (x; y), а координаты радиус-вектора
будут (x; y), а координаты радиус-вектора 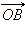 будут (x'; y'). Так как при отражении относительно прямой y = x ось абсцисс переходит в ось ординат, то абсцисса радиус-вектора
будут (x'; y'). Так как при отражении относительно прямой y = x ось абсцисс переходит в ось ординат, то абсцисса радиус-вектора 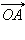 станет ординатой радиус-вектора
станет ординатой радиус-вектора 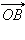 и наоборот. Следовательно, x = y', y = x'. Но координаты x и y можно найти с помощью угла α: x = cos α, y = sin α. Аналогичные формулы связывают координаты радиус-вектора
и наоборот. Следовательно, x = y', y = x'. Но координаты x и y можно найти с помощью угла α: x = cos α, y = sin α. Аналогичные формулы связывают координаты радиус-вектора 
Так как x = y' и y = x', то получаем:
Рассмотрим радиус-вектор 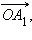 угол между которым и осью абсцисс равен –α. Очевидно, что координаты этого радиус-вектора равны (x; –y). Но абсцисса и ордината этого вектора есть синус и косинус угла –α. Следовательно,
угол между которым и осью абсцисс равен –α. Очевидно, что координаты этого радиус-вектора равны (x; –y). Но абсцисса и ордината этого вектора есть синус и косинус угла –α. Следовательно,
Отсюда легко получить, что
Последние равенства означают, что функции синус, тангенс и котангенс − нечётные, а функция косинус − чётная.
Заменим в формулах 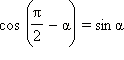 и
и 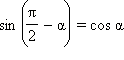 угол α на –α. Имеем
угол α на –α. Имеем
Итак, доказано, что
Выполним следующие преобразования:
Итак,
Аналогично доказываются формулы:
Из последних формул следует, что
Учтём теперь, что
Тогда из вышеприведённых формул следует:
Запишем все формулы приведения в виде таблицы.
Пример 1 Упростите выражение:
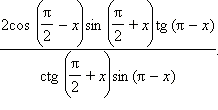
Имеем:
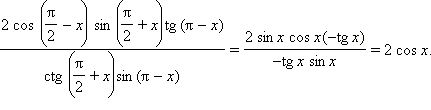
Ответ: 2 cos x.
|
Основные формулыОбратимся снова к тригонометрической окружности.
 2 2
|
| Рисунок 2.4.2.2
|
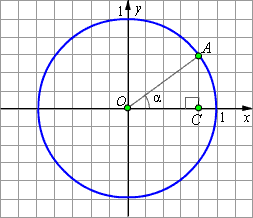
Пусть точка A является концом радиус-вектора, отвечающего углу α. Пусть также OA = 1. Построим прямоугольный треугольник AOC. Применяя к этому треугольнику теорему Пифагора, получаем:
Но OA = 1, OC = cos α, CA = sin α. Значит, непосредственным следствием теоремы Пифагора является равенство

Это равенство называется основным тригонометрическим тождеством.  |
Отсюда следует, что
Знак + или − выбирается в зависимости от того, в какой четверти лежит угол α.
Разделим основное тригонометрическое тождество на 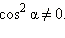 Получим:
Получим:
Разделим основное тригонометрическое тождество на 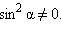 Получим:
Получим:
Из определений тангенса и котангенса 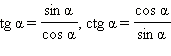 следует:
следует:
Пример 2 Найдите sin x и cos x, если 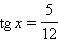 и
и 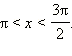
Так как 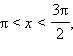 то sin x < 0 и cos x < 0. Имеем: то sin x < 0 и cos x < 0. Имеем:
Ответ. 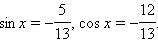
|
Пример 3 Упростить выражение:
Формулы сложения
 3 3
|
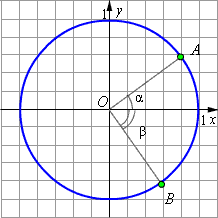
| Рисунок 2.4.2.3
|
Для вывода формул сложения для тригонометрических функций рассмотрим тригонометрическую окружность и два радиус-вектора  и
и 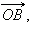 отвечающих углам α и –β (см. рис. 2.4.2.3).
отвечающих углам α и –β (см. рис. 2.4.2.3).
Координаты этих векторов по определению тригонометрических функций равны: 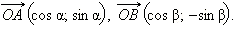 Поскольку это радиус-векторы, то их длины равны 1. Вычислим скалярное произведение этих векторов двумя способами:
Поскольку это радиус-векторы, то их длины равны 1. Вычислим скалярное произведение этих векторов двумя способами:
1. По определению.
поскольку угол между единичными векторами 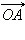 и
и 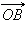 равен α + β.
равен α + β.
2. Через координаты. Имеем:
Итак, получена следующая формула сложения:
Заменим в этой формуле β на –β. Получим ещё одну формулу.
Имеем:
Значит,
Заменим в этой формуле β на –β, получим ещё одну формулу.
Из этих формул непосредственно следует, что
Последняя формула справедлива при
Эта формула справедлива при 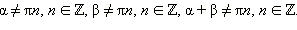
Заменяя в последних формулах β на –β, получим ещё две формулы:
Последняя формула справедлива при 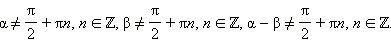
Эта формула справедлива при 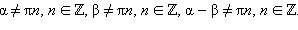
Пример 4 Упростите выражения:
1) 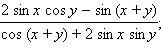
2) 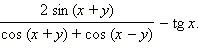
Имеем:
1) 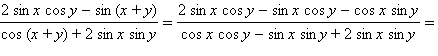

2) 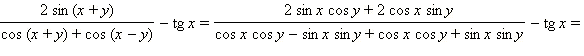
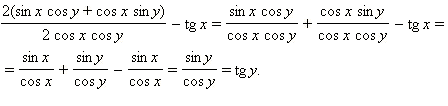
Ответ. 1) tg (x – y); 2) tg y.
|
Формулы кратного аргументаИтак, нами получены все формулы сложения для тригонометрических функций. Получим из них прямые следствия, положив в них во всех α = β.
Эти формулы называются формулами двойного угла.
Воспользуется теперь второй из этих формул и основным тригонометрическим тождеством. Получим:
Если же теперь воспользоваться формулой разности квадратов, то получится
Если в формулах сложения положить, например, β = 2α, то получим формулы кратного аргумента.
Совершенно аналогично получается формула
Полученные формулы называются формулами кратного аргумента. Аналогично можно получить формулы синуса и косинуса 4α, 5α и т. д.
Пример 5 Вычислите tg x, если 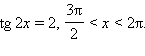
Пример 6 Упростите выражение 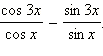
Универсальная подстановкаПерепишем теперь формулу синуса двойного угла в следующем виде:
Аналогично можно поступить с косинусом двойного угла. Получается
Разделив последнюю формулу на предпоследнюю, имеем:
Последние три формулы и формулу тангенса двойного угла часто записывают в следующем виде:
Эти формулы показывают, что все основные тригонометрические функции могут быть рационально выражены через 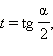 а именно:
а именно:
Говорят, что замена 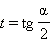 является универсальной подстановкой для основных тригонометрических функций.
является универсальной подстановкой для основных тригонометрических функций.
Формулы понижения степениИз формулы косинуса двойного угла
следуют формулы понижения степени:
Формулы половинного аргументаЕсли в последних формулах заменить α на 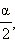 то получатся формулы половинного аргумента:
то получатся формулы половинного аргумента:
Можно получить немного другие формулы половинного аргумента для тангенса и котангенса. А именно:
Совершенно аналогично получается формула
Преобразование произведения в суммуЗапишем теперь две формулы сложения:
Сложим их:
Вычтем их:
Если рассмотреть две другие формулы сложения:
и сложить их, то получится
Три полученные формулы называются формулами преобразования произведения в сумму.
Преобразование суммы в произведениеПерепишем первую из полученных формул преобразования произведения в сумму в виде
Сделаем замену переменных: x = α – β, y = α + β. Из этой замены следует, что 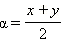 и
и 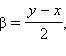 и последняя формула имеет вид
и последняя формула имеет вид
Совершенно аналогично получаются другие формулы преобразования суммы в произведение.
Пример 7 Упростите выражения
1) 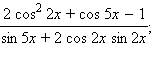
2) 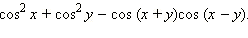
Имеем:
1) 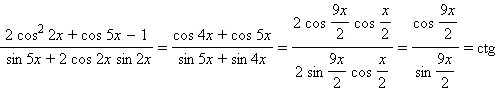 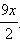
2) 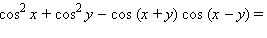
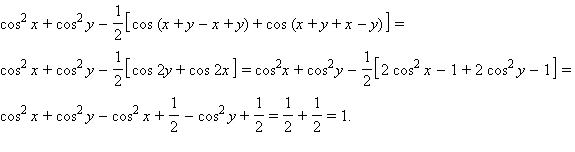
Ответ. 1)
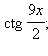 2) 1.
2) 1.
|






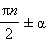 можно выражать через тригонометрические функции угла α. Эти формулы называются формулами приведения.
можно выражать через тригонометрические функции угла α. Эти формулы называются формулами приведения.
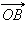 равен α.
равен α. 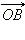 равен
равен 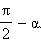 Пусть координаты радиус-вектора
Пусть координаты радиус-вектора 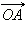 будут
будут 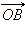 будут
будут 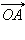 станет ординатой радиус-вектора
станет ординатой радиус-вектора 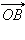 и наоборот. Следовательно,
и наоборот. Следовательно, 
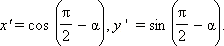
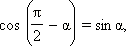
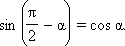
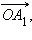 угол между которым и осью абсцисс равен –α. Очевидно, что координаты этого радиус-вектора равны
угол между которым и осью абсцисс равен –α. Очевидно, что координаты этого радиус-вектора равны 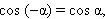
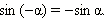
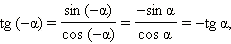
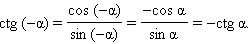
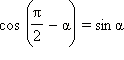 и
и 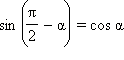 угол α на –α. Имеем
угол α на –α. Имеем
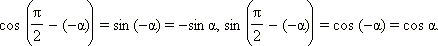
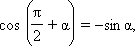
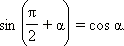
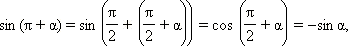
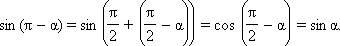
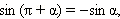
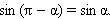
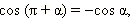
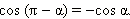
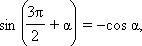
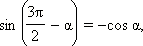
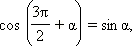
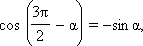
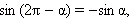
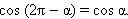
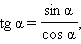
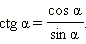

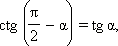
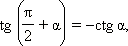

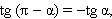
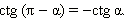

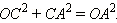
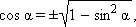
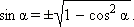
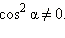 Получим:
Получим:
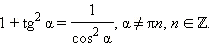
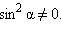 Получим:
Получим:
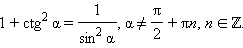
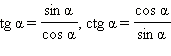 следует:
следует:
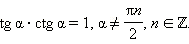

 и
и 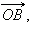 отвечающих углам α и –β (см. рис. 2.4.2.3).
отвечающих углам α и –β (см. рис. 2.4.2.3).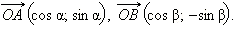 Поскольку это радиус-векторы, то их длины равны 1. Вычислим скалярное произведение этих векторов двумя способами:
Поскольку это радиус-векторы, то их длины равны 1. Вычислим скалярное произведение этих векторов двумя способами: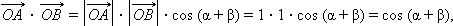
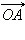 и
и 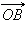 равен α + β.
равен α + β.
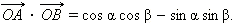
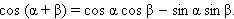

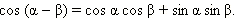


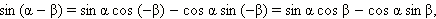
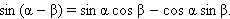
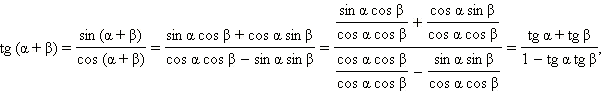
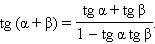
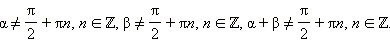
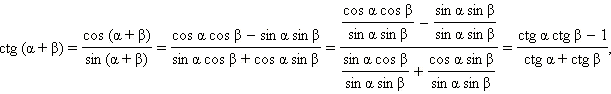
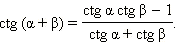
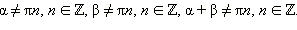
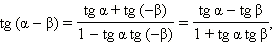
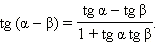
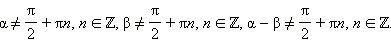
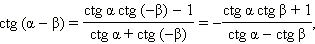
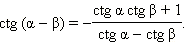
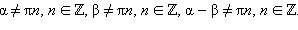
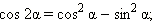
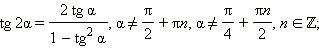
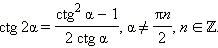
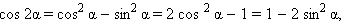
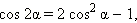
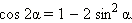
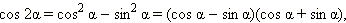
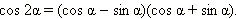
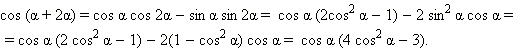
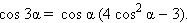
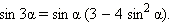
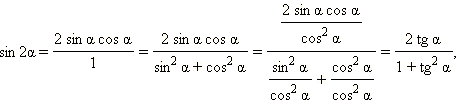
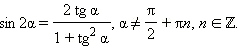
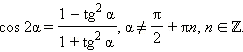
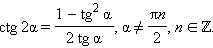
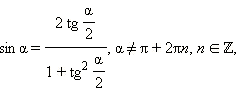
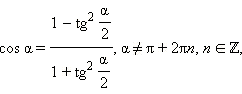
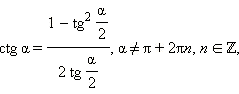
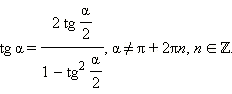
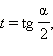 а именно:
а именно:
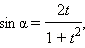
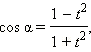
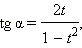
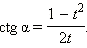
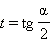 является универсальной подстановкой для основных тригонометрических функций.
является универсальной подстановкой для основных тригонометрических функций. 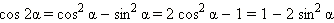
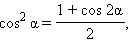
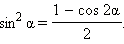
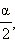 то получатся формулы половинного аргумента:
то получатся формулы половинного аргумента:
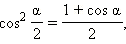
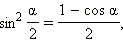
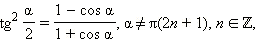
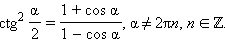
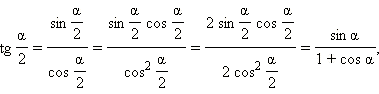
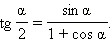
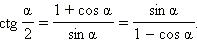
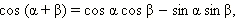
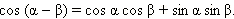
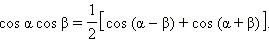
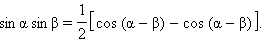

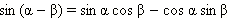
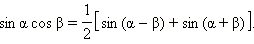
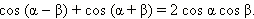
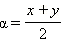 и
и 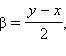 и последняя формула имеет вид
и последняя формула имеет вид