Глава 2. Алгебраические выражения
2.4.
2.4.3.
Вернемся к определению функции, данному в § 2.2.1. Отметим, что в этом определении функция f не обязана разным элементам 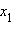 и
и 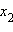 множества X ставить в соответствие разные элементы множества Y.
множества X ставить в соответствие разные элементы множества Y.
Если Y – множество значений функции f (x) и для любого элемента 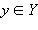 существует единственный элемент
существует единственный элемент 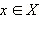 такой, что f (x) = y, то говорят, что функция осуществляет взаимнооднозначное соответствие между множествами X и Y. Другими словами, соответствие называется взаимнооднозначным, если каждому элементу
такой, что f (x) = y, то говорят, что функция осуществляет взаимнооднозначное соответствие между множествами X и Y. Другими словами, соответствие называется взаимнооднозначным, если каждому элементу 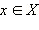 соответствует единственный элемент
соответствует единственный элемент 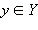 и наоборот, каждому элементу
и наоборот, каждому элементу 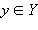 соответствует единственный элемент
соответствует единственный элемент 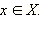 Функция, осуществляющая взаимнооднозначное соответствие, называется обратимой; ещё говорят, что у функции f существует обратная функция. Такая функция обозначается
Функция, осуществляющая взаимнооднозначное соответствие, называется обратимой; ещё говорят, что у функции f существует обратная функция. Такая функция обозначается 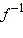 и каждому элементу
и каждому элементу 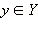 ставит в соответствие такой элемент
ставит в соответствие такой элемент 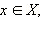 что f (x) = y; этот факт записывают так:
что f (x) = y; этот факт записывают так: 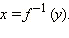 Однако нам непривычна запись функции как зависимости x от y. Поэтому сделаем формальную замену переменных
Однако нам непривычна запись функции как зависимости x от y. Поэтому сделаем формальную замену переменных 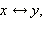 что соответствует отражению относительно биссектрисы первого и третьего координатных углов. Тогда получим, что
что соответствует отражению относительно биссектрисы первого и третьего координатных углов. Тогда получим, что 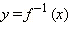 − обратная функция, график которой получается из графика исходной функции y = f (x) отражением относительно биссектрисы первого и третьего координатных углов. Область определения обратной функции совпадает с областью значений самой функции:
− обратная функция, график которой получается из графика исходной функции y = f (x) отражением относительно биссектрисы первого и третьего координатных углов. Область определения обратной функции совпадает с областью значений самой функции: 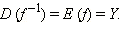 Область значений обратной функции совпадает с множеством определения самой функции:
Область значений обратной функции совпадает с множеством определения самой функции: 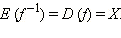
Рассмотрим функцию f (x) = sin x для 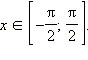 Тогда
Тогда 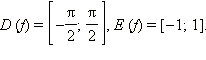 При этом область определения выбрана так, что соответствие является взаимнооднозначным. Следовательно, существует обратная функция с областью определения
При этом область определения выбрана так, что соответствие является взаимнооднозначным. Следовательно, существует обратная функция с областью определения 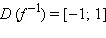 и областью значений
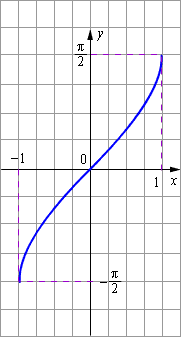
и областью значений  Эта обратная функция называется арксинусом. Её обозначение: y = arcsin x. График функции y = arcsin x изображён на рисунке.
Эта обратная функция называется арксинусом. Её обозначение: y = arcsin x. График функции y = arcsin x изображён на рисунке.
 1 1
|
| Рисунок 2.4.3.1. Арксинус |

 |
|
Модель 2.11.
Функция y = arcsin x
|
Аналогично, на промежутке D (f–1) = E (f) = [–1; 1] можно определить функцию, обратную cos x, c областью значений E (f–1) = D (f) = [0; π]
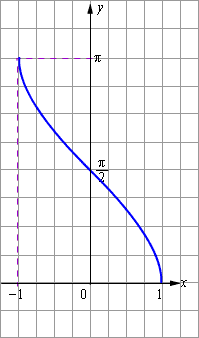
Эта обратная функция называется арккосинусом. Её обозначение: y = arccos x. График функции y = arccos x изображён на рисунке.
 2 2
|
| Рисунок 2.4.3.2. Арккосинус |

 |
|
Модель 2.12.
Функция y = arccos x
|
Рассмотрим функцию f (x) = tg x для 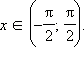 Тогда
Тогда 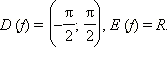 При этом область определения выбрана так, что соответствие является взаимнооднозначным. Следовательно, существует обратная функция с областью определения
При этом область определения выбрана так, что соответствие является взаимнооднозначным. Следовательно, существует обратная функция с областью определения 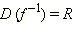 и областью значений
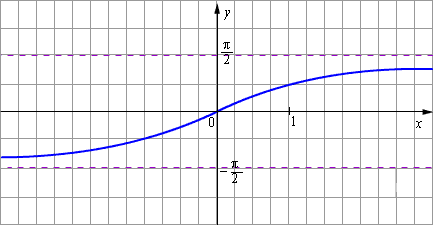
и областью значений 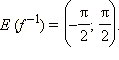 Эта обратная функция называется арктангенсом. Её обозначение y = arctg x. График функции y = arctg x изображён на рисунке.
Эта обратная функция называется арктангенсом. Её обозначение y = arctg x. График функции y = arctg x изображён на рисунке.
 3 3
|
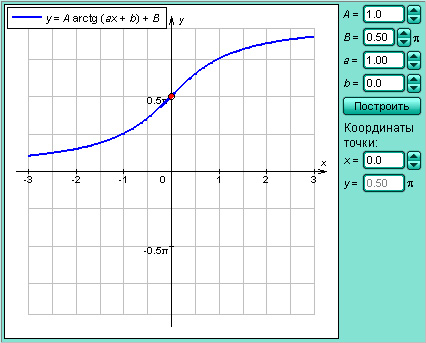
| Рисунок 2.4.3.3. Арктангенс |

 |
|
Модель 2.13.
Функция y = arctg x
|
Для построения арккотангенса выберем промежуток x  (0; π). Тогда
(0; π). Тогда 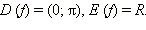 Построим обратную функцию с областью определения
Построим обратную функцию с областью определения 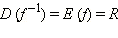 и областью значений
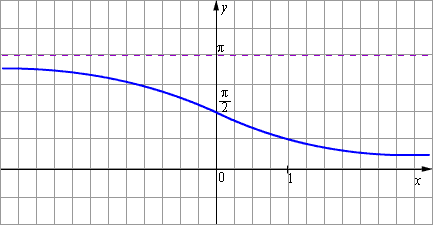
и областью значений 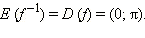 Эта обратная функция называется арккотангенсом. Её обозначение y = arcctg x. График функции y = arcctg x изображён на рисунке.
Эта обратная функция называется арккотангенсом. Её обозначение y = arcctg x. График функции y = arcctg x изображён на рисунке.
 4 4
|
| Рисунок 2.4.3.4. Арккотангенс |

 |
|
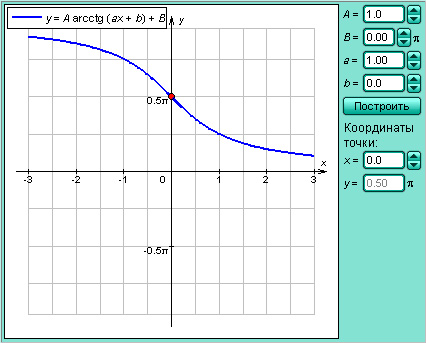
Модель 2.14.
Функция y = arcctg x
|
Итак, запись b = arcsin a обозначает, что 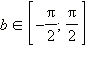 и sin b = a. Аналогичные соотношения справедливы и для остальных обратных тригонометрических функций.
и sin b = a. Аналогичные соотношения справедливы и для остальных обратных тригонометрических функций.
Пример 1Докажите тождество 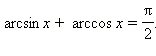
Пример 2Найти соотношение между A (x) = arcsin (cos (arcsin x)) и B (x) = arccos (sin (arccos x)).
Обозначим через y переменную, для которой выполняется равенство: 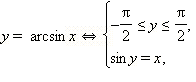 тогда cos y = cos (arcsin x). Значит,
тогда cos y = cos (arcsin x). Значит,
Здесь поставлен знак «+», поскольку y − угол первой или четвёртой четверти, в которых косинус положителен. Равенство sin (arcsin x) = x справедливо по определению функции арксинус. Значит, 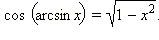
Вычислим sin (arccos x) = sin z, где 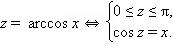 Значит,
Значит,
Здесь поставлен знак плюс, поскольку z − угол первой или второй четверти, в которых синус положителен. Равенство cos (arccos x) = x справедливо по определению функции арккосинус. Отсюда 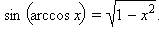
Итак,  и
и 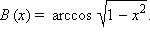 В предыдущем примере мы установили, что сумма арксинуса и арккосинуса одного и того же аргумента равна
В предыдущем примере мы установили, что сумма арксинуса и арккосинуса одного и того же аргумента равна 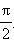 Окончательно,
Окончательно, 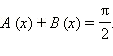
Ответ. 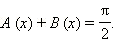
|






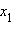 и
и 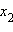 множества
множества 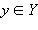 существует единственный элемент
существует единственный элемент 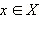 такой, что
такой, что 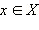 соответствует единственный элемент
соответствует единственный элемент 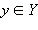 и наоборот, каждому элементу
и наоборот, каждому элементу 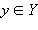 соответствует единственный элемент
соответствует единственный элемент 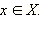 Функция, осуществляющая взаимнооднозначное соответствие, называется обратимой; ещё говорят, что у функции
Функция, осуществляющая взаимнооднозначное соответствие, называется обратимой; ещё говорят, что у функции 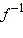 и каждому элементу
и каждому элементу 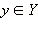 ставит в соответствие такой элемент
ставит в соответствие такой элемент 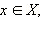 что
что 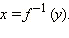 Однако нам непривычна запись функции как зависимости
Однако нам непривычна запись функции как зависимости 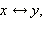 что соответствует отражению относительно биссектрисы первого и третьего координатных углов. Тогда получим, что
что соответствует отражению относительно биссектрисы первого и третьего координатных углов. Тогда получим, что 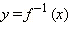 − обратная функция, график которой получается из графика исходной функции
− обратная функция, график которой получается из графика исходной функции 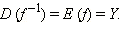 Область значений обратной функции совпадает с множеством определения самой функции:
Область значений обратной функции совпадает с множеством определения самой функции: 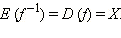
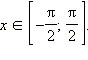 Тогда
Тогда 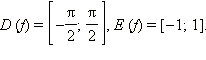 При этом область определения выбрана так, что соответствие является взаимнооднозначным. Следовательно, существует обратная функция с областью определения
При этом область определения выбрана так, что соответствие является взаимнооднозначным. Следовательно, существует обратная функция с областью определения 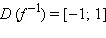 и областью значений
и областью значений  Эта обратная функция называется арксинусом. Её обозначение:
Эта обратная функция называется арксинусом. Её обозначение: 





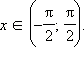 Тогда
Тогда 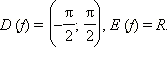 При этом область определения выбрана так, что соответствие является взаимнооднозначным. Следовательно, существует обратная функция с областью определения
При этом область определения выбрана так, что соответствие является взаимнооднозначным. Следовательно, существует обратная функция с областью определения 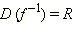 и областью значений
и областью значений 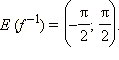 Эта обратная функция называется арктангенсом. Её обозначение
Эта обратная функция называется арктангенсом. Её обозначение 



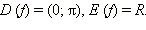 Построим обратную функцию с областью определения
Построим обратную функцию с областью определения 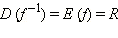 и областью значений
и областью значений 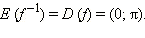 Эта обратная функция называется арккотангенсом. Её обозначение
Эта обратная функция называется арккотангенсом. Её обозначение 


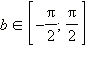 и
и 



