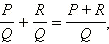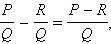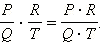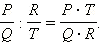Глава 2. Алгебраические выражения
2.2.
2.2.1.
Вспомним определение функции (подробнее см. курс «Открытая Математика 2.6. Функции и Графики», § 1.3.1):
Рациональной называется функция, которую можно представить в виде отношения двух многочленов, то есть 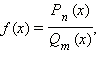 где
где 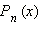 − многочлен n-ной степени,
− многочлен n-ной степени, 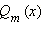 − многочлен m-ной степени. Такую функцию f (x) ещё иногда называют рациональной дробью.
− многочлен m-ной степени. Такую функцию f (x) ещё иногда называют рациональной дробью.

 |
|
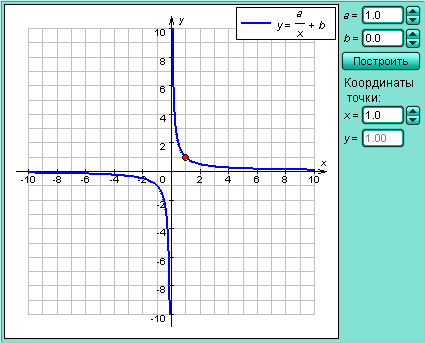
Модель 2.2.
Дробно-линейная функция
|
Пример 1
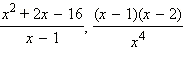 − рациональные функции;
− рациональные функции;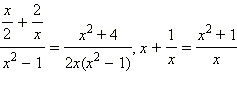 − эти функции изначально не представлены в виде отношения многочленов, но могут быть представлены в таком виде.
− эти функции изначально не представлены в виде отношения многочленов, но могут быть представлены в таком виде.
Основное свойство рациональной дроби можно выразить формулой
справедливой при 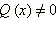 и
и 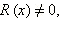 где R (x) − многочлен. Кратко основное свойство рациональной дроби может быть выражено фразой: числитель и знаменатель рациональной дроби можно умножить и разделить на одно и то же отличное от нуля число, одночлен или многочлен.
где R (x) − многочлен. Кратко основное свойство рациональной дроби может быть выражено фразой: числитель и знаменатель рациональной дроби можно умножить и разделить на одно и то же отличное от нуля число, одночлен или многочлен.
Из основного свойства рациональной дроби следуют равенства:
Например, 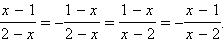
Основное свойство дроби даёт возможность умножить и разделить числитель и знаменатель рациональной дроби на одно и то же выражение, отличное от нуля. Такая операция называется сокращением дроби. Для того, чтобы сократить рациональную дробь, нужно разложить её числитель и знаменатель на множители. При этом сокращение возможно, лишь если числитель и знаменатель имеют общие множители. Если же они не имеют общих множителей, то дробь сократить нельзя.
Пример 2Сократите дробь 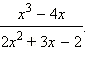
Разложим числитель и знаменатель на множители.
Числитель: x3 – 4x = x(x2 – 4) = x(x + 2)(x – 2). Мы воспользовались вынесением общего множителя за скобку и формулой разности квадратов.
Знаменатель: 
Имеем:
Ответ. 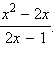
|
Для того чтобы описать действия с рациональными дробями, опишем процедуру их приведения к наименьшему общему знаменателю.
Например, общим знаменателем двух дробей 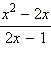 и
и 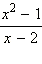 будет многочлен (x – 2)(2x – 1).
Но общим знаменателем этих дробей также служит многочлен 2x(x – 2)(2x – 1), а также
будет многочлен (x – 2)(2x – 1).
Но общим знаменателем этих дробей также служит многочлен 2x(x – 2)(2x – 1), а также 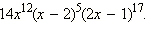 Обычно удобнее найти многочлен минимальной степени. Такой знаменатель называется наименьшим общим знаменателем. В нашем примере таким знаменателем является многочлен (x – 2)(2x – 1). Имеем:
Обычно удобнее найти многочлен минимальной степени. Такой знаменатель называется наименьшим общим знаменателем. В нашем примере таким знаменателем является многочлен (x – 2)(2x – 1). Имеем:
Множители, на которые нужно умножить числитель и знаменатель каждой дроби, называются дополнительными множителями. В нашем примере дополнительный множитель для дроби 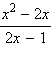 равен (x – 2), а для дроби
равен (x – 2), а для дроби 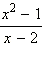 равен (2x – 1).
равен (2x – 1).
Итак, для того, чтобы привести несколько рациональных дробей к общему знаменателю, нужно:
- во-первых, разложить числитель и знаменатель каждой дроби на множители;
- во-вторых, найти общий знаменатель всех этих дробей;
- в-третьих, найти дополнительные множители для каждой дроби, они получаются путём деления общего знаменателя на знаменатель каждой из дробей;
- в-четвёртых, умножить каждую из дробей на свой дополнительный множитель.
Пример 3Привести к общему знаменателю дроби 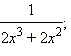
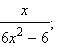
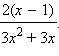
Разложим знаменатели дробей на множители:
2x3 + 2x2 = 2x2(x + 1).
6x2 – 6 = 6(x2 – 1) = 6(x + 1)(x – 1).
3x2 + 3x = 3x(x + 1).
Значит, общим знаменателем данных дробей будет многочлен 6x2(x + 1)(x – 1). Дополнительными множителями для каждой из дробей будут:
-
для первой дроби
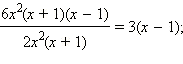
- для второй дроби
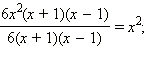
- для третьей дроби

Умножим каждую из дробей на её дополнительный множитель, приводя их тем самым к общему знаменателю:
Ответ. 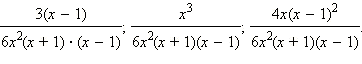
|
Перейдём теперь к изучению преобразований рациональных выражений.
Сложение. Сумма двух рациональных дробей с одинаковыми знаменателями определяется следующей формулой:
то есть для того, чтобы сложить две дроби с одинаковыми знаменателями, нужно сложить их числители, а знаменатель оставить тем же.
Вычитание. Разность двух рациональных дробей с одинаковыми знаменателями определяется следующей формулой:
то есть для того, чтобы вычесть две дроби с одинаковыми знаменателями, нужно вычесть их числители, а знаменатель оставить тем же.
Если же нужно сложить или вычесть две дроби с разными знаменателями, то сперва их следует привести к одному знаменателю и после произвести сложение и вычитание.

 |
|
Модель 2.3.
Сложение и вычитание алгебраических дробей
|
Пример 4Упростите выражение 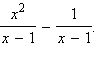
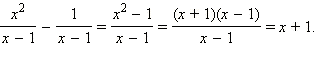
Ответ. x + 1.
|
Пример 5Упростите выражение 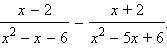
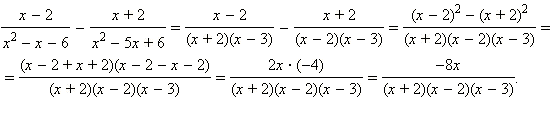
Ответ. 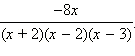
|
Умножение. Произведение двух рациональных дробей находится по следующей формуле:
Другими словами, для того, чтобы перемножить две дроби, нужно перемножить их числители и результат разделить на произведение знаменателей.
Деление. Частное двух дробей находится по следующей формуле:
Другими словами, для того, чтобы разделить одну дробь на другую, нужно первую дробь умножить на дробь, обратную второй.
Пример 6Упростите выражение 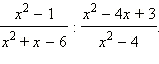
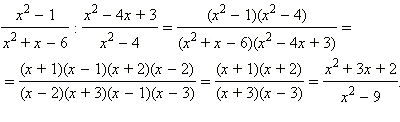
Ответ. 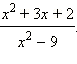
|






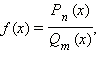 где
где 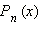 − многочлен
− многочлен 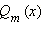 − многочлен
− многочлен 

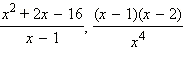 − рациональные функции;
− рациональные функции;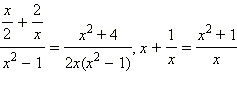 − эти функции изначально не представлены в виде отношения многочленов, но могут быть представлены в таком виде.
− эти функции изначально не представлены в виде отношения многочленов, но могут быть представлены в таком виде.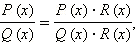
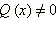 и
и 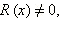 где
где 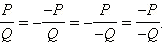
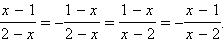




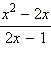 и
и 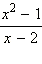 будет многочлен
будет многочлен 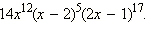 Обычно удобнее найти многочлен минимальной степени. Такой знаменатель называется наименьшим общим знаменателем. В нашем примере таким знаменателем является многочлен
Обычно удобнее найти многочлен минимальной степени. Такой знаменатель называется наименьшим общим знаменателем. В нашем примере таким знаменателем является многочлен 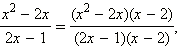
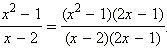
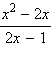 равен
равен 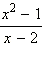 равен
равен