Данный многочлен имеет целые коэффициенты. Если целое число является корнем этого многочлена, то оно является делителем числа 16. Таким образом, если у данного многочлена есть целые корни, то это могут быть только числа ±1; ±2; ±4; ±8; ±16. Непосредственной проверкой убеждаемся, что число 2 является корнем этого многочлена, то есть x3 – 5x2 – 2x + 16 = (x – 2)Q(x), где Q(x) − многочлен второй степени. Следовательно, многочлен разлагается на множители, один из которых (x – 2). Для поиска вида многочлена Q(x) воспользуемся так называемой схемой Горнера. Основным преимуществом этого метода является компактность записи и возможность быстрого деления многочлена на двучлен. По сути, схема Горнера является другой формой записи метода группировки, хотя, в отличие от последнего, является совершенно ненаглядной. Ответ (разложение на множители) тут получается сам собой, и мы не видим самого процесса его получения. Мы не будем заниматься строгим обоснованием схемы Горнера, а лишь покажем, как она работает.
В прямоугольную таблицу
2 × (n + 2) , где
n − степень многочлена, (см. рис.) в верхнюю строчку выписываются подряд коэффициенты многочлена (левый верхний угол при этом оставляют свободным). В нижний левый угол записывают число − корень многочлена (или число
x0, если мы хотим разделить на двучлен (
x – x0)), в нашем примере это число 2. Далее вся нижняя строчка таблицы заполняется по следующему правилу.
Во вторую клетку нижней строки «сносится» число из клетки над ней, то есть 1. Затем поступают так. Корень уравнения (число 2) умножают на последнее написанное число (1) и складывают результат с числом, которое стоит в верхнем ряду над следующей свободной клеткой, в нашем примере имеем:
Результат записывается в свободную клетку под тем числом, с которым только что производилось сложение, то есть под −5.
Далее корень 2 умножается на последнюю написанную цифру, то есть на −3, и складывается с числом, которое стоит в верхнем ряду над следующей свободной клеткой, то есть −2; имеем:
Результат пишем в свободную клетку под −2. Далее поступаем аналогично:
В последней клетке (правый нижний угол), если нигде не совершено ошибки и 2 − действительно корень данного многочлена, должен получиться нуль. Это признак правильного решения. В общем случае в этой клетке оказывается остаток от деления исходного многочлена на
(x – 2) (в нашем примере). У нас получился 0, следовательно, 2 − действительно корень этого многочлена.
Полученные числа 1, −3, −8 являются коэффициентами многочлена, который получается при делении исходного многочлена на x – 2. Значит, результат деления:
| 1 · x2 + (–3)x + (–8) = x2 – 3x – 8. |
Степень многочлена, полученного в результате деления, всегда на 1 меньше, чем степень исходного. Итак:
| x3 – 5x2 – 2x + 16 = (x – 2)(x2 – 3x – 8). |
Корни многочлена второй степени ищутся легко уже описанным выше способом (по формуле корней) и равны:
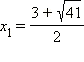
и
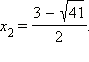
Окончательно:
Ответ. 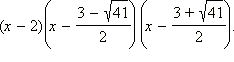




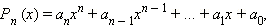
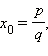 то число
то число 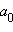 (свободного члена), а число
(свободного члена), а число 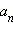 (старшего коэффициента).
(старшего коэффициента).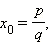 где
где 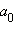 (свободного члена), а число
(свободного члена), а число 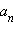 (старшего коэффициента).
(старшего коэффициента).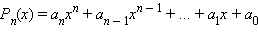 являются целыми числами, и пусть целое число
являются целыми числами, и пусть целое число 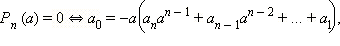 то отсюда следует, что коэффициент
то отсюда следует, что коэффициент 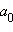 делится на
делится на 



