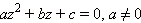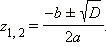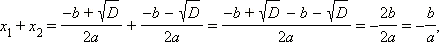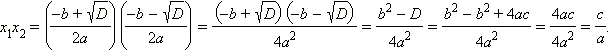Глава 2. Алгебраические выражения
2.1.
2.1.4.
Общая теория многочленов многих переменных далеко выходит за рамки школьного курса. Поэтому мы ограничимся изучением многочленов одной действительной переменной, да и то в простейших случаях. Рассмотрим многочлены одной переменной, приведённые к стандартному виду.
 |
 |
 |
|
|
Вообще, многочлен
| Pn(x) = anxn + an – 1xn – 1 + an – 2xn – 2 + ... + a1x + a0, |
где 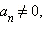 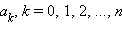
− числа, x − переменная, называется многочленом n-ной степени. Традиционно 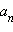
называется старшим коэффициентом, а 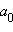
− свободным членом многочлена.
|
 |
 |
 |
 |
|
В дальнейшем мы будем рассматривать многочлены с действительными коэффициентами.

 |
|
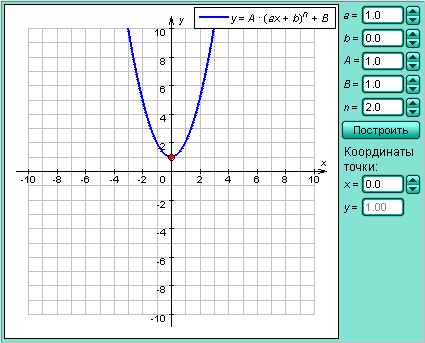
Модель 2.1.
Степенная функция
|
Корень многочлена первой степени легко угадывается: 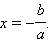 В самом деле:
В самом деле: 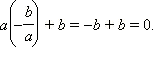
Корни квадратного трехчлена можно найти, если воспользоваться так называемым методом выделения полного квадрата. Его суть проще всего увидеть на примере. Выполним следующие преобразования квадратного трехчлена:
Выражение D = b2 – 4ac называется дискриминантом квадратного трехчлена. Продолжим преобразования в предположении, что D ≥ 0:
Воспользуемся теперь формулой сокращённого умножения для разности квадратов.
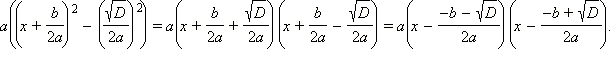
Обозначим 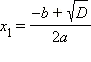 и
и 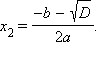 Тогда последнее разложение квадратного трехчлена имеет вид:
Тогда последнее разложение квадратного трехчлена имеет вид:
| ax2 + bx + c = a(x – x1)(x – x2). |
Отсюда непосредственно видно, что числа x1 и x2 являются корнями квадратного трехчлена ax2 + bx + c. Полученная формула ввиду своей важности называется формулой разложения квадратного трехчлена на множители.
Итак, установлено, что если D ≥ 0, то квадратный трехчлен имеет два корня (при D = 0 они совпадают). Если же D < 0, то трехчлен не имеет действительных корней.
Пример 1Разложить на множители квадратный трехчлен x2 – 4x + 3.
Несмотря на то, что в дальнейшем, рассматривая многочлены, мы будем искать только действительные корни, сделаем в этом разделе небольшое отступление и покажем, что у квадратного трехчлена при любом D существуют два, в общем случае комплексных, корня. Аналогично, у любого многочлена степени n на множестве комплексных чисел есть n корней, некоторые из них могут совпадать.
Пользуясь понятием комплексного числа как расширения понятия числа действительного, можно найти корни квадратного трехчлена и при D < 0. Итак, на множестве комплексных чисел квадратное уравнение:
всегда имеет два комплексных корня:
 Очевидно, что при условии, что a, b, c – действительные числа, корнями квадратного трехчлена могут быть:
- два различных действительных числа;
- одно действительное число;
- сопряженные комплексные числа.
 |
Пример 2Решите уравнение 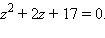
Вычисляем дискриминант: 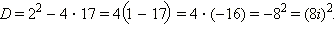
Формула корней даёт: 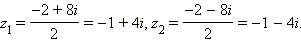
Ответ. 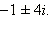
|
Для того чтобы установить одну важную теорему, касающуюся квадратного трехчлена, вычислим следующие комбинации корней этой функции:
Итак, нами доказана следующая теорема, принадлежащая великому французскому математику Виету.
Пример 3Пусть 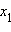 и
и 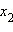 − корни квадратичной функции
− корни квадратичной функции 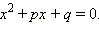 Найти, чему равно значение выражения
Найти, чему равно значение выражения 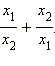
Так как x1 и x2 − корни квадратичной функции x2 + px + q = 0, то справедливы соотношения:
Тогда имеем: 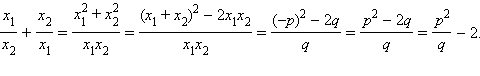
Ответ. 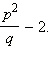
|




























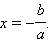 В самом деле:
В самом деле: 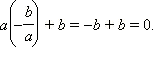
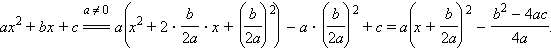
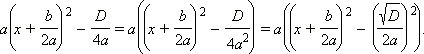
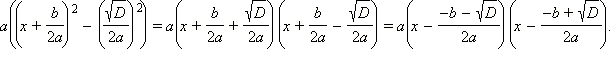
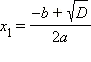 и
и 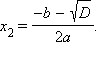 Тогда последнее разложение квадратного трехчлена имеет вид:
Тогда последнее разложение квадратного трехчлена имеет вид:
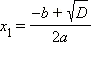 и
и 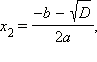
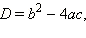 в том случае, если
в том случае, если