

 |
 |
В § 1.1.2 было определено понятие степени натурального числа с натуральным показателем. Обобщим это определение на случай произвольного действительного числа.
 |
 |
|
 |
 |
|
Справедливы следующие свойства степени:
|
Например, 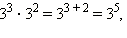
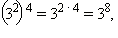

По определению полагают, что
 |
 |
||
|
По определению полагают, что если
|
|||
 |
 |
||
Справедливо равенство 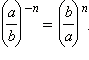 Например,
Например, 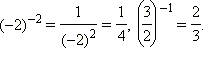
Совершенно аналогично вводится понятие степени рациональных выражений. Чтобы возвести рациональную дробь в натуральную степень, нужно отдельно возвести в эту степень числитель, и отдельно − знаменатель:
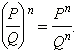 |
Возведение рациональной дроби в отрицательную степень происходит по следующей формуле:
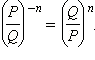
 |
 |
 |

