Глава 2. Алгебраические выражения
2.2.
2.2.3.
Вместо слова «корень» часто говорят радикал. Если n = 2, то обычно пишут просто: 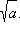 При n = 2 арифметический корень называется квадратным корнем, при n = 3 говорят о кубическом корне.
При n = 2 арифметический корень называется квадратным корнем, при n = 3 говорят о кубическом корне.
Итак, по определению:
Отсюда следует, что 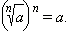 Например,
Например, 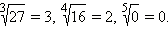
Если a < 0, а 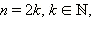 то не существует такого действительного x, при котором бы выполнялось равенство
то не существует такого действительного x, при котором бы выполнялось равенство 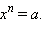 Следовательно, невозможно ввести понятие корня чётной степени из отрицательного числа. Однако определить понятие корня нечётной степени из отрицательного числа всё же возможно. В самом деле, пусть a < 0, а n − нечётное число, тогда существует единственное число x такое, что
Следовательно, невозможно ввести понятие корня чётной степени из отрицательного числа. Однако определить понятие корня нечётной степени из отрицательного числа всё же возможно. В самом деле, пусть a < 0, а n − нечётное число, тогда существует единственное число x такое, что 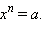 Это число и называется корнем нечётной степени из отрицательного числа. Оно обозначается точно так же:
Это число и называется корнем нечётной степени из отрицательного числа. Оно обозначается точно так же: 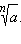 Например,
Например, 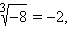 так как
так как 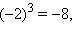
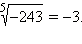 Для нечётных показателей степени свойства, справедливые для неотрицательных значений подкоренных выражений, верны также и для отрицательных значений подкоренных выражений.
Для нечётных показателей степени свойства, справедливые для неотрицательных значений подкоренных выражений, верны также и для отрицательных значений подкоренных выражений.










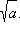 При
При 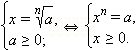
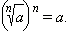 Например,
Например, 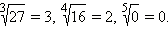
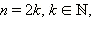 то не существует такого действительного
то не существует такого действительного 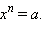 Следовательно, невозможно ввести понятие корня чётной степени из отрицательного числа. Однако определить понятие корня нечётной степени из отрицательного числа всё же возможно. В самом деле, пусть
Следовательно, невозможно ввести понятие корня чётной степени из отрицательного числа. Однако определить понятие корня нечётной степени из отрицательного числа всё же возможно. В самом деле, пусть 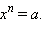 Это число и называется корнем нечётной степени из отрицательного числа. Оно обозначается точно так же:
Это число и называется корнем нечётной степени из отрицательного числа. Оно обозначается точно так же: 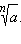 Например,
Например, 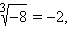 так как
так как 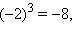
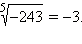 Для нечётных показателей степени свойства, справедливые для неотрицательных значений подкоренных выражений, верны также и для отрицательных значений подкоренных выражений.
Для нечётных показателей степени свойства, справедливые для неотрицательных значений подкоренных выражений, верны также и для отрицательных значений подкоренных выражений.



