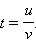Глава 3. Решение уравнений и неравенств
3.1.
3.1.10.
Найдём условие, при котором будут равны синусы двух углов. Пусть sin a = sin b. Тогда sin a – sin b = 0, и по известной формуле разности синусов имеем
Значит, либо 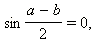 то есть
то есть 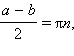
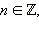 либо
либо 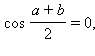 то есть
то есть 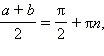
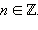 Итак, sin a = sin b тогда и только тогда, когда либо a – b = 2πn, либо a + b = (2n + 1)π,
Итак, sin a = sin b тогда и только тогда, когда либо a – b = 2πn, либо a + b = (2n + 1)π, 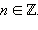
Рассмотрим решение простейшего уравнения sin x = a. Если |a| > 1, то решений нет, если |a| ≤ 1, то в силу периодичности синуса решений будет бесконечно много. По определению обратных тригонометрических функций, одно из решений − это arcsin a. Следовательно, наше уравнение можно переписать в виде sin x = sin (arcsin a). Тогда либо x – arcsin a = 2πn, 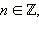 либо x + arcsin a = 2(n + 1)π,
либо x + arcsin a = 2(n + 1)π, 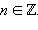 Оба эти равенства могут быть объединены в одно:
Оба эти равенства могут быть объединены в одно:
Это равенство называется формулой общего решения уравнения sin x = a, |a| ≤ 1.
Аналогично можно показать, что формула общего решения уравнения cos x = a при |a| ≤ 1 имеет вид
Формула общего решения уравнения tg x = a при любом действительном a имеет вид
x = arctg a + πn, 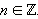 |
Формула общего решения уравнения ctg x = a при любом действительном a имеет вид
x = arcctg a + πn, 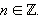 |
Рассмотренные уравнения называются простейшими тригонометрическими уравнениями.

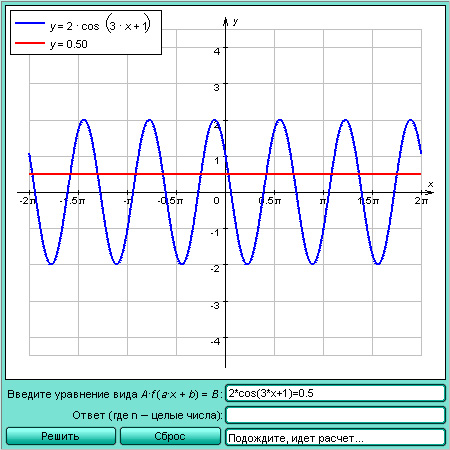 |
|
Модель 3.5.
Простейшие тригонометрические уравнения
|
Пример 1Решите уравнение sin 2x = cos 3x.
Воспользуемся формулой приведения 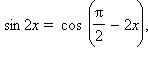 получаем
получаем
По формуле разности синусов имеем
Следовательно, либо 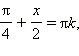
то есть 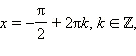
либо 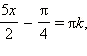
то есть 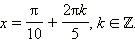
Ответ. 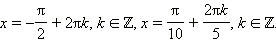
|
Пример 2Решите уравнение sin x – 2 cos x = 0.
Преобразуем уравнение sin x = 2 cos x. Рассмотрим те x, для которых cos x = 0. Для этих x sin x = ±1. Следовательно, эти x не являются корнями исходного уравнения, так как при их подстановке получается неверное числовое равенство 0 = ±1. Значит, cos x ≠ 0. Разделим обе части уравнения на cos x ≠ 0, имеем tg x = 2, x = arctg 2 + πn, 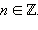
Ответ. x = arctg 2 + πn, 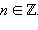
|
Пример 3Решите уравнение sin2 x – 6 sin x cos x + 5 cos2 x = 0.
Те значения переменной x, для которых cos x = 0, не являются решениями, в чём можно убедиться непосредственной подстановкой. Разделим обе части уравнения на cos2 x, получим
Это уравнение является квадратным относительно переменной t = tg x:
Корни этого уравнения: 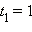
и 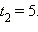
Уравнение 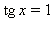
имеет решения 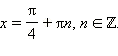
Уравнение tg x = 5 имеет решения 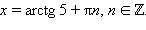
Ответ. 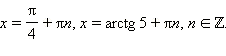
|
Только что рассмотренные уравнения называются однородными уравнениями соответственно 1-го и 2-го порядка. Вспомним определение многочлена n-ной степени, данное в § 2.1.1. Однородным многочленом n-ного порядка относительно переменных u и v называется многочлен, у которого сумма степеней переменных постоянна у всех членов.
Аналогично, уравнения au + bu = 0 и au2 + bvu + cv2 = 0 также называются однородными уравнениями 1-го и 2-го порядка. В нашем случае было u = sin x и v = cos x.
Уравнение 1-го порядка делением на v сводится к линейному относительно новой переменной 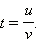 Уравнения 2-го порядка делением на
Уравнения 2-го порядка делением на 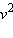 сводятся к квадратному относительно
сводятся к квадратному относительно 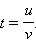
Уравнения с обратными тригонометрическими функциями, как правило, удаётся решить, применяя одну и ту же тригонометрическую функцию к обеим частям данного уравнения.
Пример 4Решите уравнение arccos x = arctg x.
Применим функцию косинус к обеим частям данного уравнения. Имеем  Так как область определения данного уравнения − множество
Так как область определения данного уравнения − множество 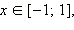 то:
то:
Значит, x > 0. Решаем полученное иррациональное уравнение:
Так как x > 0, то 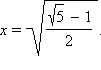
Ответ. 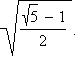
|






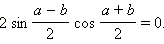
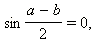 то есть
то есть 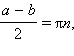
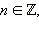 либо
либо 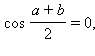 то есть
то есть 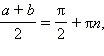
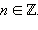 Итак,
Итак, 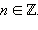
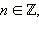 либо
либо 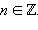 Оба эти равенства могут быть объединены в одно:
Оба эти равенства могут быть объединены в одно:
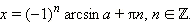

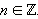
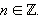


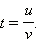 Уравнения 2-го порядка делением на
Уравнения 2-го порядка делением на 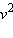 сводятся к квадратному относительно
сводятся к квадратному относительно