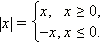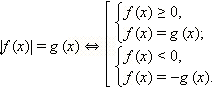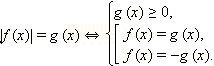Все корни исходного уравнения содержатся среди корней двух уравнений
которые можно переписать в виде
|
|
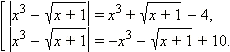 |
(*)
|
Аналогично, каждое из этих уравнений распадается на два:
что приводит к четырём уравнениям:
Отсюда получаем 4 решения: 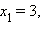
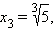
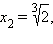
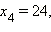 среди которых содержатся корни исходного уравнения. 1-й корень, очевидно, удовлетворяет уравнению. Это проверяется легко. 2-й и 3-й не походят, так как правая часть исходного уравнения при этих значениях отрицательна. 4-й корень тоже является лишним, так как этот корень должен удовлетворять уравнению (*), а при этом значении его правая часть отрицательна.
среди которых содержатся корни исходного уравнения. 1-й корень, очевидно, удовлетворяет уравнению. Это проверяется легко. 2-й и 3-й не походят, так как правая часть исходного уравнения при этих значениях отрицательна. 4-й корень тоже является лишним, так как этот корень должен удовлетворять уравнению (*), а при этом значении его правая часть отрицательна.
Ответ. 3.