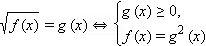Глава 3. Решение уравнений и неравенств
3.1.
3.1.7.
Очевидно, что вне ОДЗ решений не существует, однако не все числа, входящие в ОДЗ, служат решениями уравнения.
Уравнение можно решить и не находя ОДЗ. С другой стороны, верно найденное ОДЗ и последующий отбор корней с его помощью не может гарантировать отсутствие ошибок.
Приведём два примера, принадлежащих И. Ф. Шарыгину, показывающих, что нахождение ОДЗ может быть как чрезвычайно сложной с одной стороны, так и абсолютно необходимой, с другой стороны, задачей.
Пример 1Решите уравнение 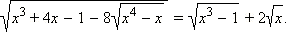
Совершенно понятно, что поиск ОДЗ в данном примере сопряжён с огромными трудностями. Однако попробуем решить это уравнение непосредственно. Поскольку мы будем лишь возводить в квадрат, то ОДЗ может лишь расшириться, то есть могут появиться посторонние корни. Однако эти корни мы можем отсеять проверкой. Имеем:
Проверкой убеждаемся, что из двух найденных корней подходит только 1. Так как при возведении в квадрат мы не могли потерять решения, а могли только их приобрести, то 1 и есть окончательный ответ.
Ответ. 1.
|
Пример 2Решите уравнение 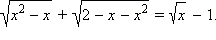
В этом примере наоборот сложно его решение. Однако поиск ОДЗ приносит несомненную пользу. В самом деле, ОДЗ:
Значит, ОДЗ нашего уравнения содержит только два числа. А поскольку вне ОДЗ решений быть не может, то корнями нашего уравнения могут быть только эти два числа. Для того чтобы понять, какое из них действительно является решением, нужно полученные числа подставить в уравнение. Подстановка даёт, что x = 0 не является решением уравнения, а x = 1 − является.
Ответ. 1.
|
Таким образом, к понятию ОДЗ нужно относиться творчески и искать его, только если в этом возникает существенная необходимость. Так, например, в равносильном переходе
требование g (x) ≥ 0 задаёт ОДЗ. Однако, если искать g (x) очень сложно, то проще подставить найденные корни в исходное уравнение, чем выяснять, при каких x выполнено неравенство g (x) ≥ 0.