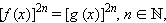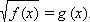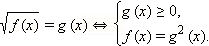Глава 3. Решение уравнений и неравенств
3.1.
3.1.6.
Эту теорему также называют основной теоремой алгебры. Согласно этой теореме, уравнение (*) имеет хотя бы один корень z = z0. Разделив многочлен, стоящий в левой части (*) на одночлен (z = z0), мы получим снова уравнение вида (*), которое согласно той же теореме Гаусса имеет хотя бы одно решение. Продолжая так n раз, получим следствие теоремы Гаусса: любое алгебраическое уравнение n-ной степени имеет ровно n, вообще говоря, комплексных, корней (разумеется, некоторые корни могут совпадать).
Пример 1Решите уравнение z3 + z – 2 = 0.
Очевидно, z = 1 – корень этого уравнения. Разделив многочлен z3 + z – 2 на одночлен (z – 1), например, по схеме Горнера, получим разложение исходного многочлена на множители:
Корни квадратичной функции находим по формуле корней квадратного уравнения:
Ответ. 1, 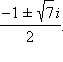
|
Рациональные уравнения являются следующим по сложности типом стандартных уравнений.
Для решения дробно-рациональных уравнений существует алгоритм.
1. Найти общий знаменатель дробей, входящих в уравнение.
2. Заменить данное уравнение уравнением с целыми коэффициентами, умножив его на общий знаменатель.
3. Попытаться решить полученное уравнение с целыми коэффициентами.
4. Исключить из его корней те, которые обращают в нуль общий знаменатель.
5. Записать ответ.
Пример 2Решите уравнение 
Общий знаменатель дробей, входящих в уравнение, есть (x – 1)(x + 2). Умножая на него обе части уравнения, получим 3x(x + 2) – 2x(x – 1) = 3x + 2. Последнее уравнение сводится к квадратному уравнению x2 + 5x + 6 = 0, корни которого x = –3 и x = –2. Подставляя эти числа в общий знаменатель дробей исходного уравнения, убеждаемся, что при x = –2 он обращается в нуль, при x = –3 знаменатель нулю не равен. Значит, x = –2 не является корнем уравнения.
Ответ. x = –3.
|
Стандартным методом их решения является возведение уравнения в подходящую степень. Однако, как следует из § 3.1.1, возведение уравнения в произвольную степень не всегда приводит к равносильному уравнению.
Действительно, уравнение
|
|
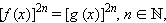 |
(6)
|
является лишь следствием уравнения f (x) = g (x), то есть содержит все корни этого уравнения, но может иметь и другие корни. Уравнение (6) среди своих корней содержит ещё и корни уравнения f (x) = –g (x) (если таковые существуют), следствием которого оно также является. Итак, у уравнения (6) «больше» корней, чем у уравнения f (x) = g (x), а это как раз и обозначает, что при возведении в чётную степень могут появиться посторонние корни. В этом случае проверка необходима, как составляющий элемент решения. Она необходима даже в тех случаях, когда лишние корни не появились, но ход решения был таков, что они могли появиться. В последнем случае иногда проще сделать проверку, чем доказать, что она не нужна. Именно поэтому проверка здесь является элементом решения.
К тому же, проверка может быть средством контроля правильности проделанных вычислений. Однако проверить полученные корни подстановкой не всегда легко. Лишние корни, которые могли появиться при возведении уравнения, например, в квадрат, могут быть отсеяны на основе следующего соображения.
Рассмотрим уравнение
|
|
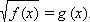 |
(7)
|
Ясно, что если x = x0 − решение этого уравнения, то обе части этого равенства при x = x0 должны быть неотрицательны. Следовательно, потребовав дополнительно, чтобы g(x) ≥ 0, уравнение можно возвести в квадрат. Имеем следующее соотношение равносильности:
|
|
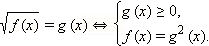 |
(8)
|
Система (8) действительно является равносильной уравнению (7). В самом деле, из системы (8) следует, что функция f (x) равна полному квадрату функции g (x), то есть для решения является неотрицательной.
Пример 3Решите уравнение 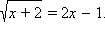
Перейдём сразу к равносильной системе.
Ответ. 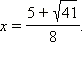
|