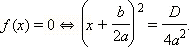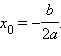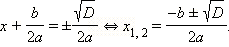Глава 3. Решение уравнений и неравенств
3.1.
3.1.5.
Если a = 0, то уравнение примет вид bx + c = 0 и будет уравнением степени не выше первой, которое рассмотрено выше.
Если a ≠ 0, то уравнение рассматриваемого вида называется квадратным уравнением (или уравнением второй степени).
Обозначим f (x) = ax2 + bx + c и зададимся целью решить уравнение
| f (x) = ax2 + bx + c = 0, a ≠ 0. |
Разложение квадратного трехчлена на множители было произведено в § 2.1.4:
Следующим существенным шагом является извлечение арифметического квадратного корня из обеих частей полученного уравнения, но поскольку дискриминант может иметь разные знаки, то возникает три случая:
- Если D < 0, то действительных корней нет.
- Если D = 0, то корни совпадают и равны
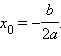
- Если D > 0, то, извлекая корень, получим
Это и есть формула для решения квадратного уравнения.
Пример 1Решите уравнение x2 + 2x – 3 = 0.
Вычислим дискриминант этого уравнения: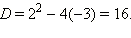 
Следовательно, по формуле корней квадратного уравнения можно сразу получить, что 
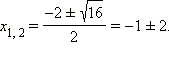Значит,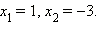 
Ответ. 1, −3.
|
Пример 2Решите уравнение x2 + 6x + 9 = 0.
Вычисляя дискриминант этого уравнения, получим, что D = 0 и, следовательно, это уравнение имеет один корень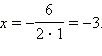 
Однако можно поступить проще, заметив, что в левой части данного уравнения стоит полный квадрат: 
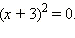Отсюда равенство x = –3 получается сразу.
Ответ. x = –3.
|
Пример 3Решите уравнение x2 + 2x + 17 = 0.
Вычислим дискриминант этого уравнения: D = 22 – 4 · 17 = –64 < 0. Следовательно, данное уравнение действительных корней не имеет.
Ответ. Решений нет.
|
